
Table of Contents
Market makers, equipped with high-frequency trading capabilities, low-cost structures, and real-time creation/redemption privileges, are the primary participants in ETF premium–discount arbitrage.
In contrast, retail investors face multiple constraints—information delays, transaction fees, and taxes—which make it difficult for them to enter the market promptly or profit effectively, even when an arbitrage opportunity is detected.
Using the Yuanta Taiwan 50 ETF (0050) as an example, this study simulates the actual execution of premium–discount arbitrage by these two market participants based on historical data.
By comparing performance under varying entry/exit thresholds and cost structures—and evaluating metrics such as win rate, return distribution, and drawdown risk—we aim to clarify an essential question:In this seemingly “risk-free arbitrage,” who truly captures the opportunity and earns consistent profits?
An ETF’s market price is determined by investors buying and selling on the exchange, while its net asset value (NAV) reflects the actual value of the assets held by the fund. When market demand changes suddenly or when there is a timing gap in the pricing of the underlying assets, the ETF’s trading price may deviate from its NAV, resulting in a “discount” or “premium.”
To keep the ETF’s price close to its NAV, market makers and authorized participants (APs) can conduct arbitrage through the creation and redemption mechanism. For example, when an ETF trades at a premium, a market maker can simultaneously sell the ETF and buy the basket of underlying assets, then redeem the ETF at NAV to earn the arbitrage spread. Conversely, when the ETF trades at a discount, the opposite operation can be performed.
Such arbitrage mechanisms help prices return to fair value and improve market efficiency. However, in practice, arbitrage opportunities often vanish quickly. Successful arbitrage relies not only on real-time quotes and high-speed execution, but is also constrained by transaction fees, taxes, and liquidity conditions—creating very different practical challenges for different types of market participants.
This study uses December 31, 2020 as the data cut-off date to divide the historical dataset into training and testing sets, thereby avoiding look-ahead bias during the parameter estimation stage. The backtesting target is the 0050 ETF, and the arbitrage logic is based on the premium/discount between the ETF’s market price and its net asset value (NAV).
For entry and exit decisions, only the premium/discount ratio in the training set is used to compute the mean and standard deviation, which serve as the decision threshold. When the daily premium/discount ratio deviates significantly from the training-period mean by more than one standard deviation, it is regarded as a signal that short-term price imbalance has occurred, triggering an arbitrage action: if the market price is clearly undervalued relative to NAV, the strategy buys the ETF and sells the corresponding basket of constituent stocks; the opposite is performed when the ETF appears overvalued.
Through this simplified yet executable strategy design, this study aims to isolate and analyze the potential differences between market makers and retail investors in actual arbitrage execution within a real-world market structure.
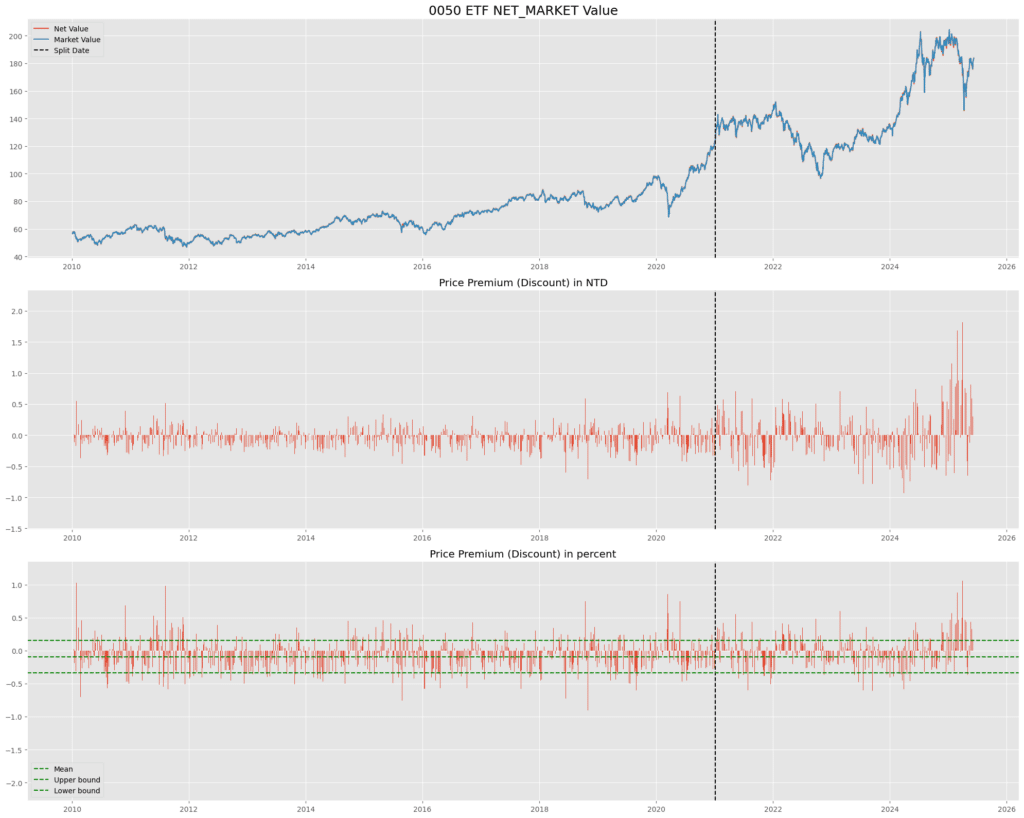
This study adopts the premium/discount ratio as the criterion for determining entry and exit points, rather than the absolute premium/discount spread. The main reason is that the absolute spread changes with the ETF’s price level, causing deviations of the same percentage magnitude to appear larger when the ETF’s price is high.
For example, in the case of the 0050 ETF, when its price rises above NT$150, a seemingly modest premium or discount ratio of 1%–2% can translate into a spread of NT$1–2. Although the spread appears substantial in absolute terms, the deviation relative to NAV is actually quite small.
Therefore, using the ratio provides a more accurate reflection of the true arbitrage opportunity, without distortion caused by changes in the ETF’s price level.
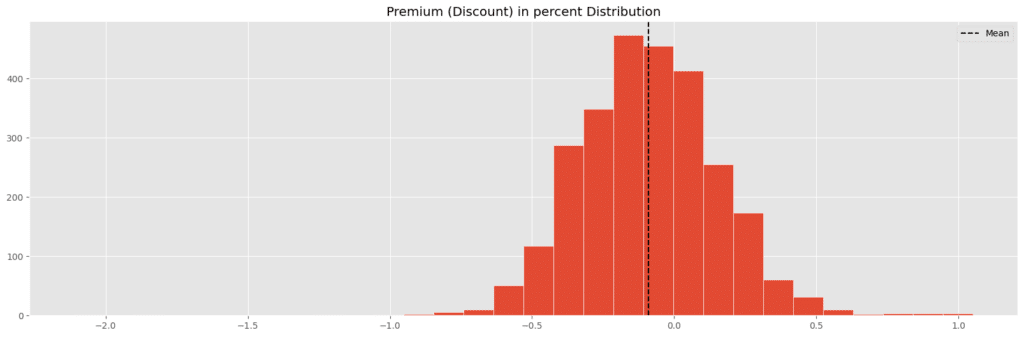
To differentiate the perspectives of market makers and retail investors, the key distinction lies in the presence or absence of trading costs. For ordinary investors, arbitrage opportunities become attractive only when the price deviation is sufficiently large to cover transaction fees and taxes. In contrast, market makers are primarily responsible for providing liquidity and maintaining price stability in the ETF market, rather than maximizing arbitrage profits.
Accordingly, in this study, I set a three-standard-deviation threshold as the entry criterion for retail investors, reflecting the need for a larger mispricing before an arbitrage trade becomes worthwhile. For market makers, the entry threshold is set at one standard deviation, consistent with their lower cost structure and their role in promptly correcting ETF mispricings.
In this study, we adopt a relatively loose entry threshold—one standard deviation—to represent how market makers intervene to stabilize ETF prices. Because market makers are exempt from securities transaction taxes and trading commissions when providing liquidity, they are able to act on smaller arbitrage deviations without being constrained by high costs. For comparison, we also illustrate how cumulative returns would appear if the same one-standard-deviation threshold were applied with transaction costs included, highlighting the significant performance gap between market makers and regular investors.
To evaluate the strategy’s performance, we implement a return-calculation framework that decomposes the arbitrage position into two components: the NAV leg (based on the ETF’s net asset value) and the MV leg (based on the ETF’s market trading price). The strategy determines long or short positions on each leg based on the daily trading signal.
When a long signal is triggered on the previous day—indicating entry into a long arbitrage position—the following day records a positive return on the NAV side (long NAV) and a negative return on the MV side (short MV). This setup reflects the logic of ETF arbitrage, where market makers generally buy the underlying basket (NAV) and short the ETF (MV), profiting from price convergence when premiums shrink.
Conversely, when a short signal occurs, the strategy enters a short arbitrage position. In this case, the NAV leg contributes a negative return (short NAV), while the MV leg contributes a positive return (long MV), capturing gains when discounts narrow. If no signal is generated, both components remain inactive and record zero return.
After computing the daily returns for each leg, the framework accumulates them over time to construct the cumulative return curves for both the NAV and MV sides. The daily total strategy return is obtained by summing NAV and MV returns, and its cumulative value reflects the overall performance of the arbitrage strategy.
This implementation provides a precise breakdown of where profits originate—allowing us to observe, for example, whether returns primarily come from market-price mean reversion or from NAV adjustment—and enables a clear assessment of the strategy’s long-term viability. By combining both the structural advantages of market makers and the mechanics of the arbitrage process, this analysis highlights why market makers can execute such strategies consistently, while regular investors often see their returns offset by transaction costs.
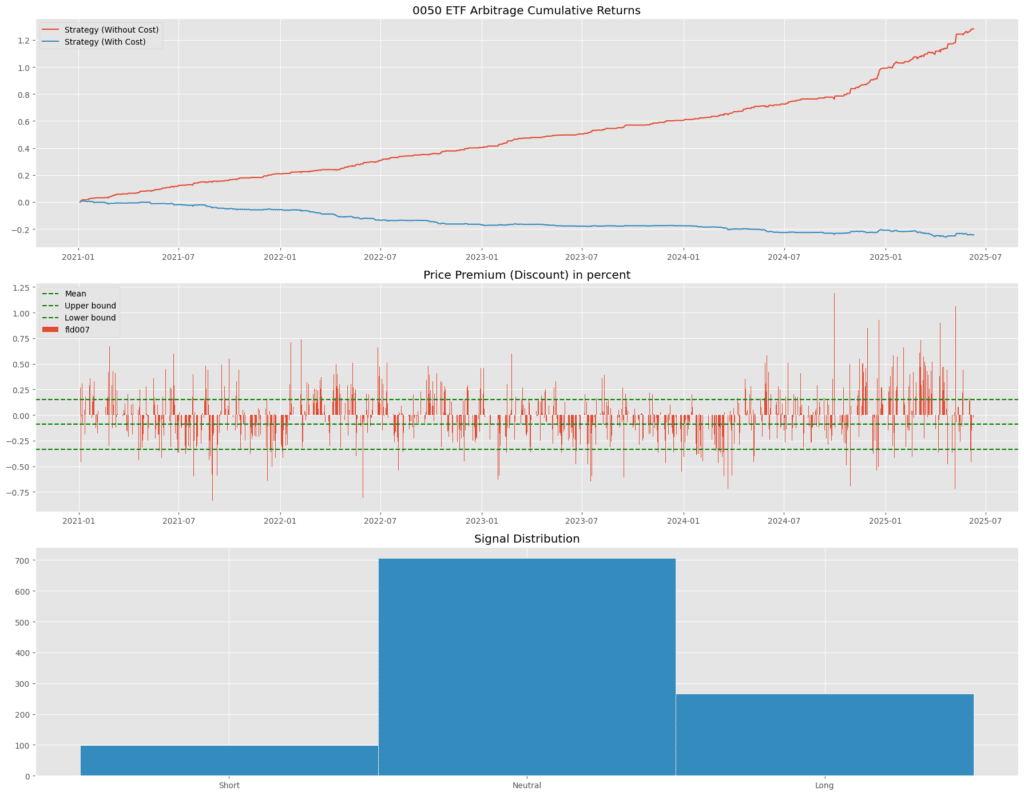
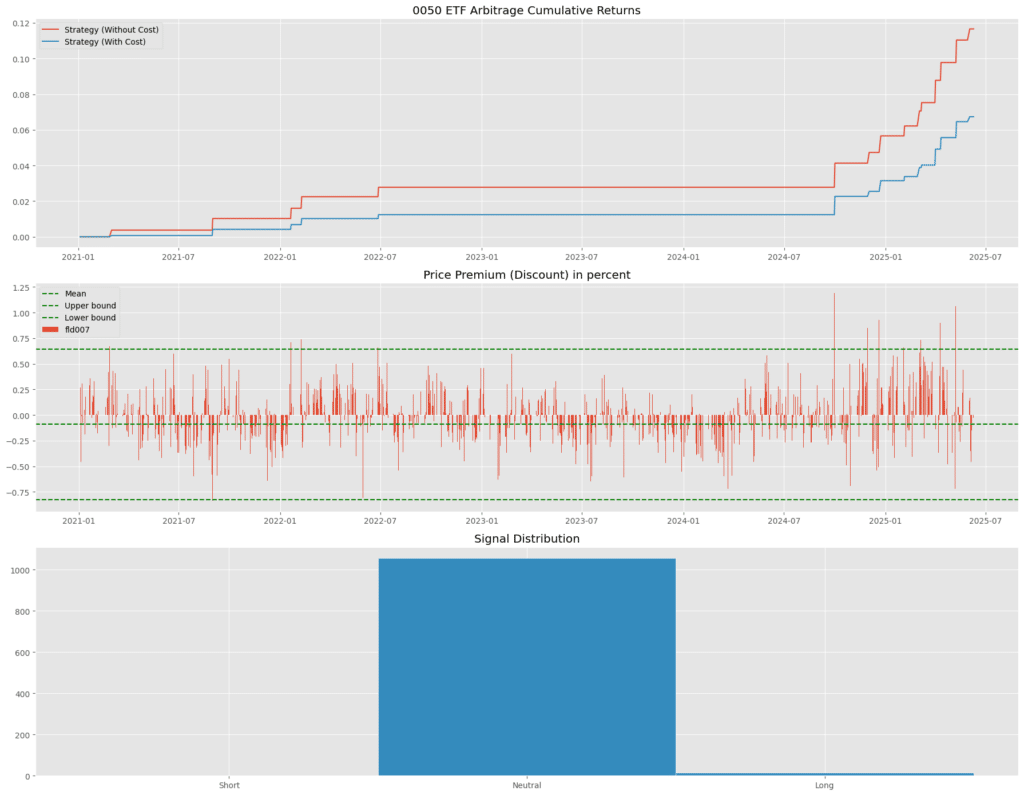
From the red line in the first subplot, we observe the cumulative return of the one-standard-deviation strategy without transaction costs, representing the perspective of a market maker. The results suggest that this arbitrage strategy can generate some profits for market makers, although the returns are far from excessive. At the same time, such profits are not the primary objective for market makers; their main role is to maintain ETF price stability and provide market liquidity. Therefore, the returns shown in the chart can be viewed more as a form of indirect benefit.
Looking at the blue line in the same subplot, which represents cumulative returns after accounting for transaction costs, we can clearly see that once trading costs are included, the cumulative returns decline almost linearly. This illustrates that retail investors cannot replicate the market maker’s trades, as most of the potential arbitrage profits would be entirely eroded by transaction fees—often resulting in overall losses.
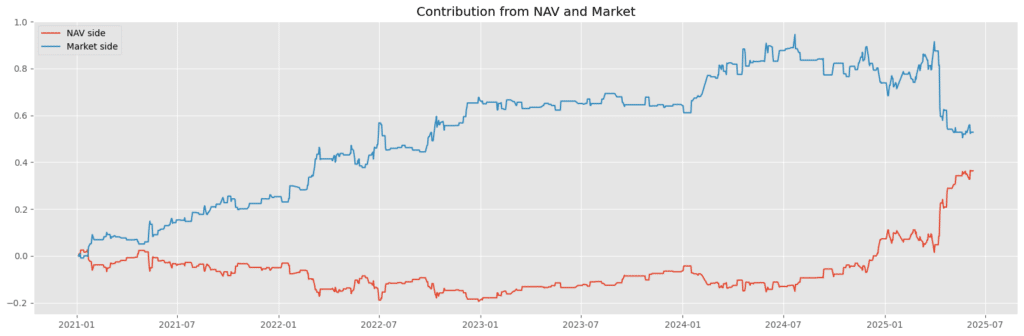
This figure illustrates the cumulative return contributions from both the NAV leg and the market-price leg of the strategy. It is evident that the majority of the profits are generated on the market-price side, indicating a stronger mean-reversion tendency in the ETF’s market price. In contrast, the NAV side shows relatively unstable contributions and is negative for most periods.
This phenomenon aligns with real-world market mechanics: when an ETF displays a premium or discount, the prices of its underlying constituents typically adjust before the ETF market price does. As a result, the eventual arbitrage profit primarily comes from the market price converging back toward NAV.

Based on the figure above, retail investors cannot operate using the same entry criteria as market makers, because high transaction costs would erode most of the returns. Therefore, we tighten the entry threshold and adopt three standard deviations as the signal for retail investors. Since the premium/discount ratio must exceed three standard deviations to trigger a trade, each individual trade is expected to generate a higher return compared to the one-standard-deviation strategy. The higher return should allow investors to retain some profit even after paying transaction fees. However, the number of trading opportunities will decrease correspondingly.

From the figure, we observe that after tightening the entry threshold to three standard deviations, the number of trading opportunities decreases significantly. However, the trades that do occur tend to yield relatively stable returns. Despite this improvement, the overall cumulative return reaches only about 12%. After accounting for transaction costs, the net cumulative return drops to approximately 7%. This indicates that even with stricter entry criteria, the resulting performance is still not attractive enough for general investors to adopt the strategy.
Moreover, the opportunities to enter trades are extremely limited. As shown in the first subplot, there are no valid entry signals before July 2024, with all opportunities concentrated only after that point. For most investors, allocating funds to lower-risk bond assets over the same period—earning returns primarily through coupon payments—would likely outperform the three-standard-deviation arbitrage strategy.
| Project | Market makers (one standard deviation) | Typical investor (three standard deviations) |
| winning rate | 100% | 100% |
| average profit | 0.00385 | 0.00739 |
| average loss | – | – |
| reward factor | – | – |
You are welcome to explore the analysis presented here. In future articles, I will continue demonstrating how to use the TEJ database to construct various financial indicators and perform backtesting on different trading strategies. For readers who are interested in systematic trading or quantitative backtesting, I highly recommend exploring the TQuant Lab plans — a high-quality data infrastructure can help you build strategies that truly fit your investment style.
A gentle reminder: this analysis is for informational and educational purposes only. It does not constitute any form of financial advice or investment recommendation.
【TQuant Lab Backtesting System】Solving Your Quantitative Finance Pain Points
The backtesting period spans from 2010 to 2025.
From the results, using the market maker’s perspective (first subplot), adopting a lower entry threshold—such as one standard deviation—captures the highest returns, as there are no transaction costs or taxes involved. This indicates that market makers can consistently earn profits while providing liquidity to the ETF market. These profits primarily arise from exploiting short-term market inefficiencies.
From the retail investor’s perspective (second subplot), using a two-standard-deviation threshold yields the highest returns. Although other thresholds (except one standard deviation) also generate profits, the return levels are not particularly attractive. For example, the best-performing line (the purple line) only achieves a cumulative return of around 40% over 15 years, which translates to an annualized return of roughly 2.7%. This level of performance is generally insufficient to motivate most investors to engage in such arbitrage strategies.
TEJ Knowledge Finance Academy officially presents — “TQuantLab: Introduction to Quantitative Investing”.
This course integrates TEJ’s empirical data with practical quantitative methods, guiding you from the fundamentals to the core concepts of quantitative investment. Whether you are a finance professional, an investment researcher, or someone looking to enhance your analytical thinking, this course helps you build systemized research and evaluation skills—fast and effectively!
TQuantLab — Your gateway to effective quantitative investing.