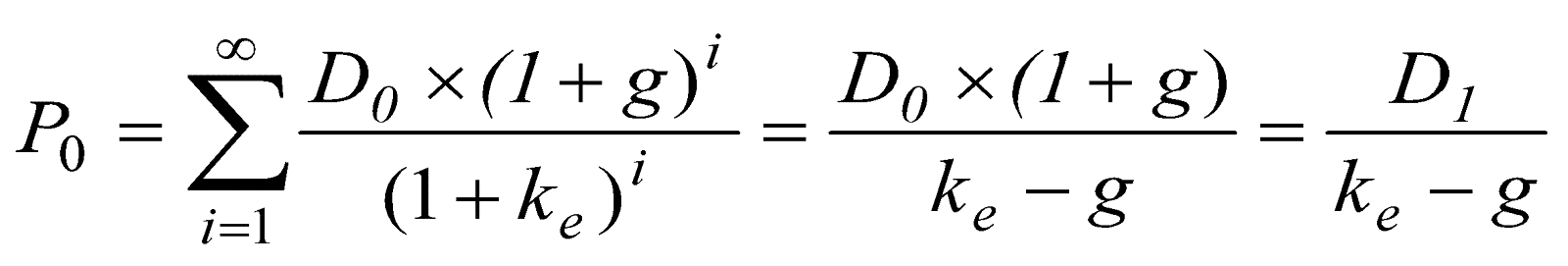內容目錄
收益法是將未來金額(現金流量或收益費損)予以折現，取得之現值。
FVM教材對收益法之指引，以「現金流量折現法(Discounted Cash Flow method, DCF)」為核心，兼及「股利折現模式(Dividend Discount Model, DDM)」，與兩個簡化模式：固定成長DDM(Constant-growth DDM)、固定成長DCF―資本化模式(Capitalization model)。
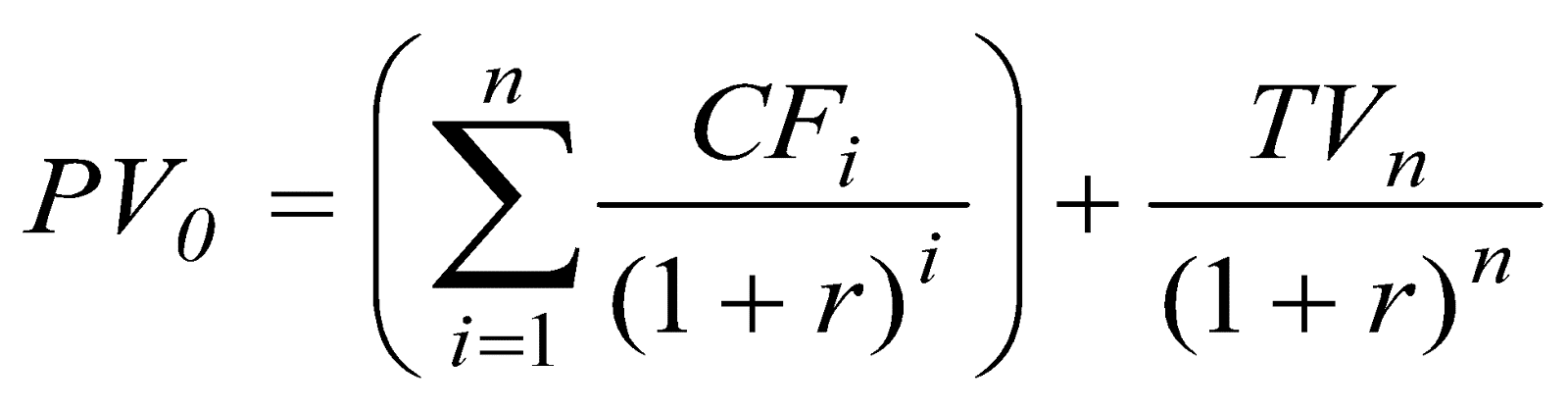。計算現值時，必須先決定三個部分:CF現金流量(cash flow)、r折現率、TV終值(terminal value)，需特別注意的是，CF現金流量(cash flow)是營業現金流量CFO扣除維持成長必要的資本支出(reinvestment requirements, RR)與搭配投入的淨營運資金增額，即「自由現金流量(Free Cash Flow, FCF)」。
DCF在不同評價基礎下的變數比較，如表一所列。
| 基礎 | 企業價值基礎(間接) | 權益價值基礎(直接) |
| 對象 | 權益持有者+債權人 | 權益持有者 |
| 現金流量 | 公司自由現金流量（FCFF），係公司支付了所有營運費用及必需的固定資產與營運資產投資後，可以向所有投資者分派的現金流量 | 股權自由現金流量(FCFE)，是公司自由現金流量(FCFF)扣除借款之利息費用及本金清償，加上新增融資款=FCFF−利息費用*(1-企業所得稅稅率)−本金清償+新增融資款 |
| 折現率 | 加權平均資金成本（WACC），按各種資金結構比率加權平均計算的資金總成本 | 權益資金成本( )(股東預期之投資報酬率) |
資料來源：FVM教材，Figure 4。
各變數之公式如下：
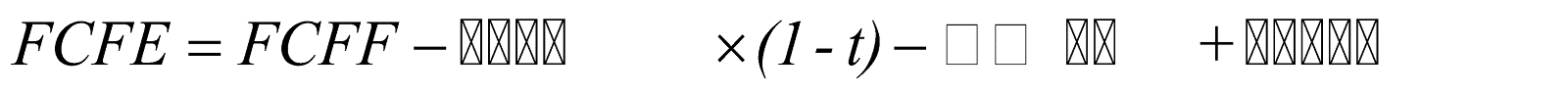
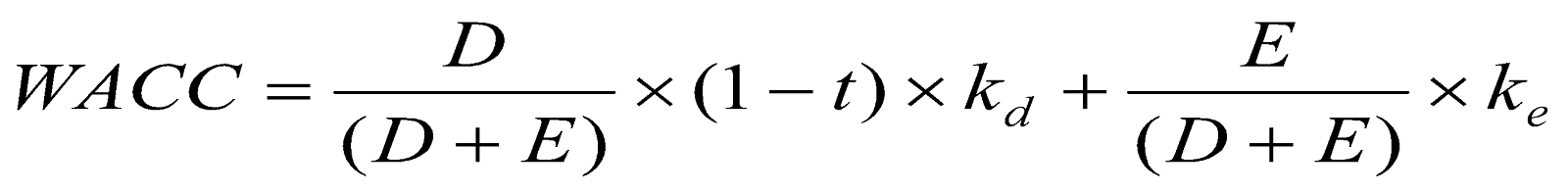
其中：
：債務資金成本
：權益資金成本至於終值(TV)，以資本化模式計算，列式如下：
採企業價值評價基礎，CF係自由現金流量（FCFF）、折現率r係加權平均資金成本（WACC），因此終值(TV)計算公式為： 
採股權評價基礎，CF係自由現金流量（FCFE）、折現率r係權益資金成本()，因此終值(TV)計算公式為：：
其中：g為終值之永久性成長率
但須注意，由於未來營運現金流量之預估，不包含非營運資產負債之營運績效，因此，需再加上非營運之資產與負債，才能得到完整的企業價值(或是股權價值)。
及)之計算在針對現金流量折現時，挑選適當的折現率極為重要，一般而言，多數人選擇使用標準的資本資產訂價模式(Capital Assets Pricing Model, CAPM) 或其簡單的變異。
FVM教材，對於權益資金成本（）的估計如下：
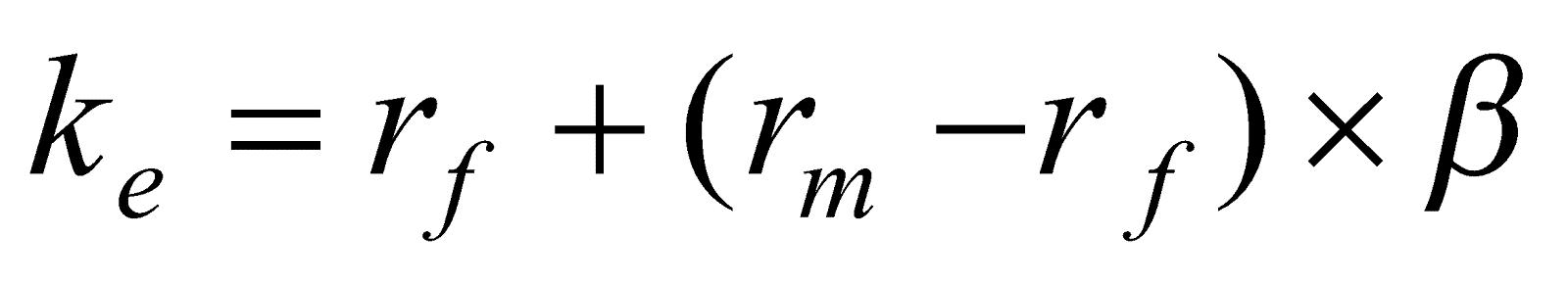
其中，
：無風險利率(risk-free rate)，對無風險資產期望的報酬率；
：投資人要求的市場報酬率(required market rate of return)，
對一個充分風險分散之投資組合之預期報酬率；
：投資人要求的風險貼水(required equity premium)；
：單一資產的系統風險係數。
係將各變數分別說明於下：
(1-1)無風險利率()
在進行股票評價時，針對無風險利率，國外多採用10年期或20年期的公債殖利率，因股票產生的現金流量的存續期間長。在我國多採用台灣政府10年期公債殖利率，主因10年期公債的交易非常活絡。
(1-2)風險係數(β)
β應為前瞻性 (forward-looking estimate)，而非歷史β。常見以歷史β作為替代，所隱含的假設是：未來的波動與過去類似。
運用迴歸推估歷史β時，期間長短決定於所搭配的資料頻率與資料品質：
若年度夠長，採月資料、週資料頻率即可(原則上，日資料噪音過大)。一般來說，會採用過去2-5年的歷史資料推估β；若僅用2年資料，多採週報酬；若估計期長達5年，就可能採月報酬。若市場波動過大，就會拉長期間，以免受短期波動之扭曲。
(1-3)未上市櫃公司之β
由於β代表的風險有兩類：營運風險與財務風險。可類比公司僅是營運風險類似（有相似之風險、成長及現金流量特性），財務風險則未必。因此，在借用可類比公司之β時，若長期資本結構(財務風險之主要指標)差異太大時，就該用Hamada公式來調整差異，有兩個步驟：
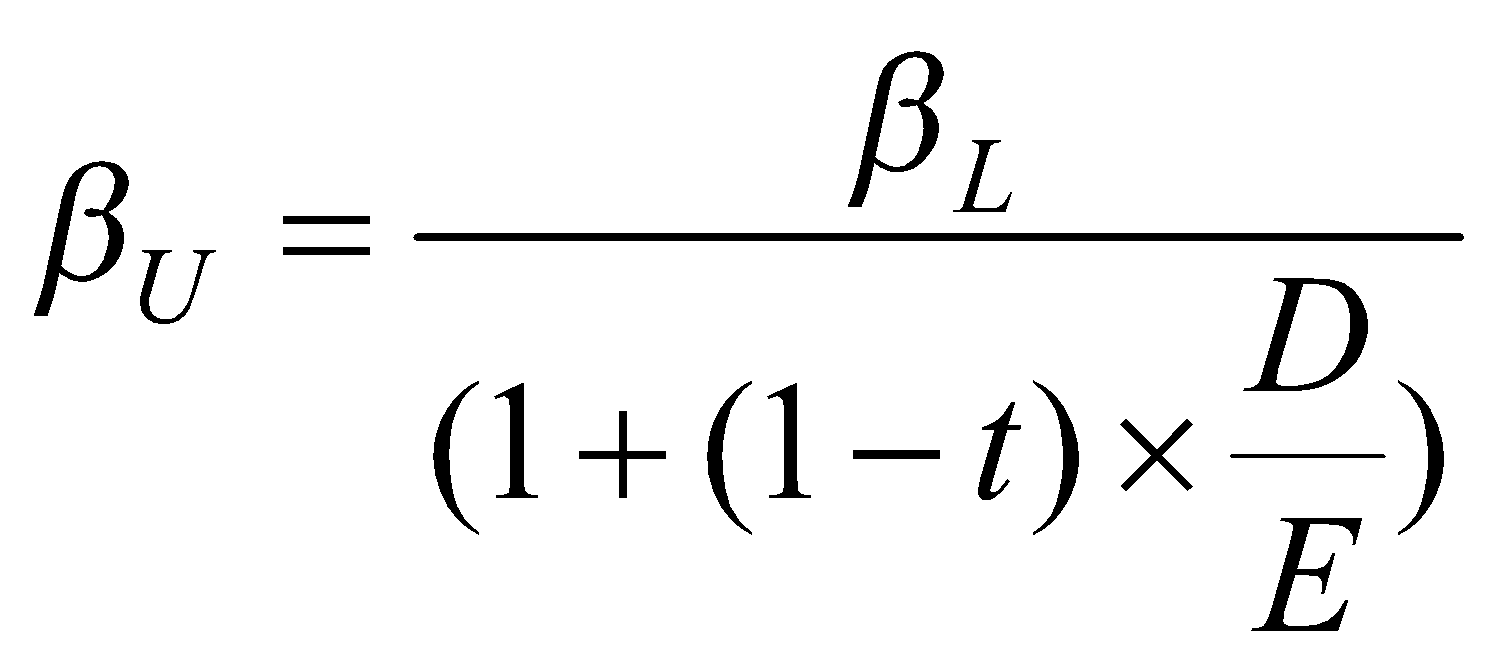
其中，
：無舉債時的β；
：有舉債時的β；
D ：債務之公允價值；
E ：股東權益之公允價值。
後，就可推估未上市櫃公司的
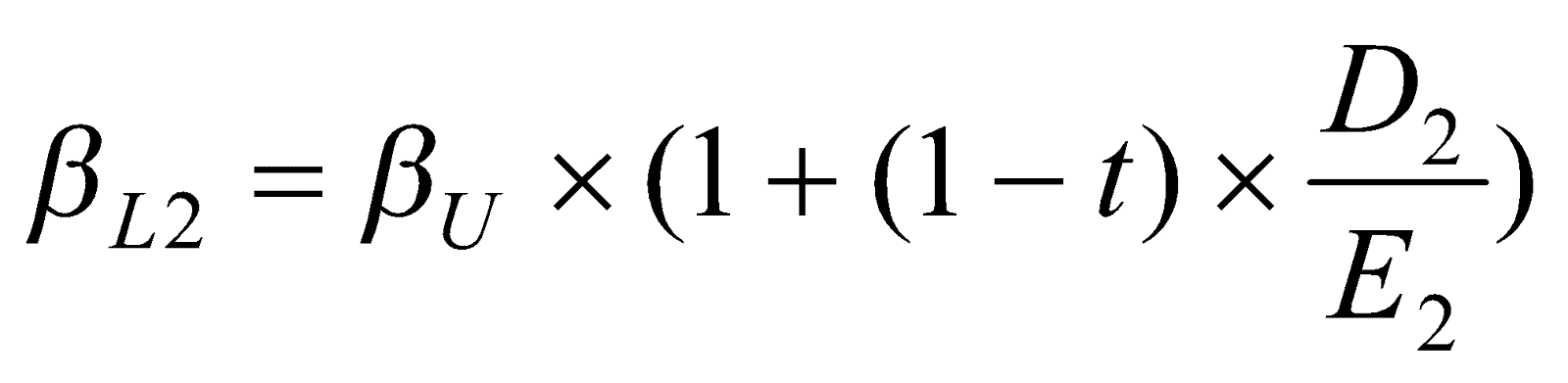
其中，
：未上市櫃公司債務之公允價值；
：未上市櫃公司股東權益之公允價值。
(1-4)投資人要求的風險貼水()
市場期望的風險貼水，也是前瞻性，理應由歷史資料作為推估起點。但FVM教材對新興市場的推估說明，係以成熟市場作推估。
(2)債務資金成本()
相對於權益資金成本，債務資金成本就簡單得多。可用近期舉債成本(recent borrowing)作為推估起點，也可採信用價差作長期推估。不管採取何種方式，總要符合市場參與者的長期最適之預期。如果目前的財務結構接近長期最適的財務結構，則可用近期舉債成本，作為推估起點。原則上，要加上增額借款、再融資之考量，也可參考可類比公司之資料。
(3)債務比重――長期最適財務結構
由於評價是公司的長期價值，因此WACC所用的權重(債務比率)並非現時的狀況，而是公司理想的財務結構。通常，可採用產業平均的財務結構。但若該被投資公司之融資能力、信用狀況與產業差異甚大時，就得另行調整。
若FCFF會以一個固定比率永續成長，資金成本也是一個常數，則其評價就可簡化成：
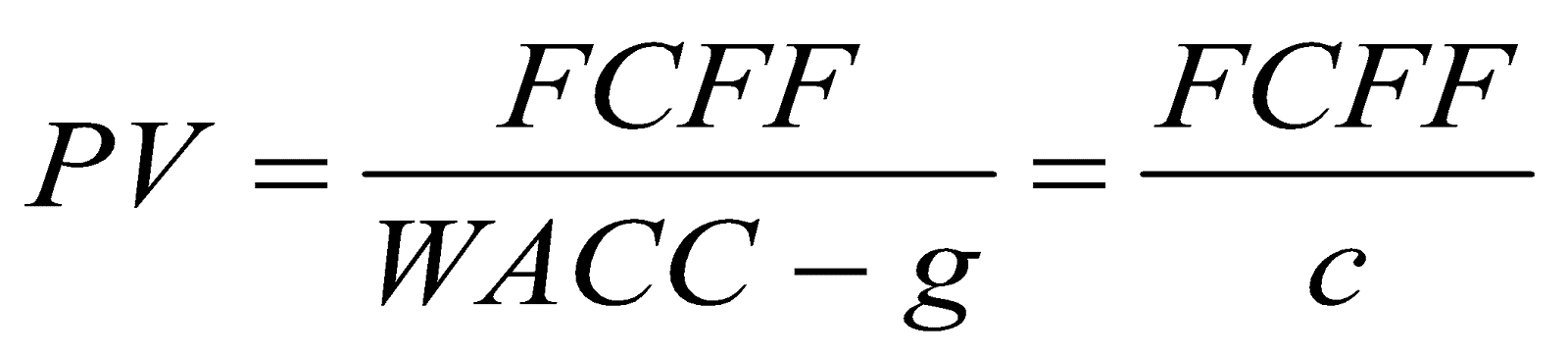
基本觀點是「今天的股價就是未來現金股利之折現總和」，並假設公司一定會發放股利，其估算如下：
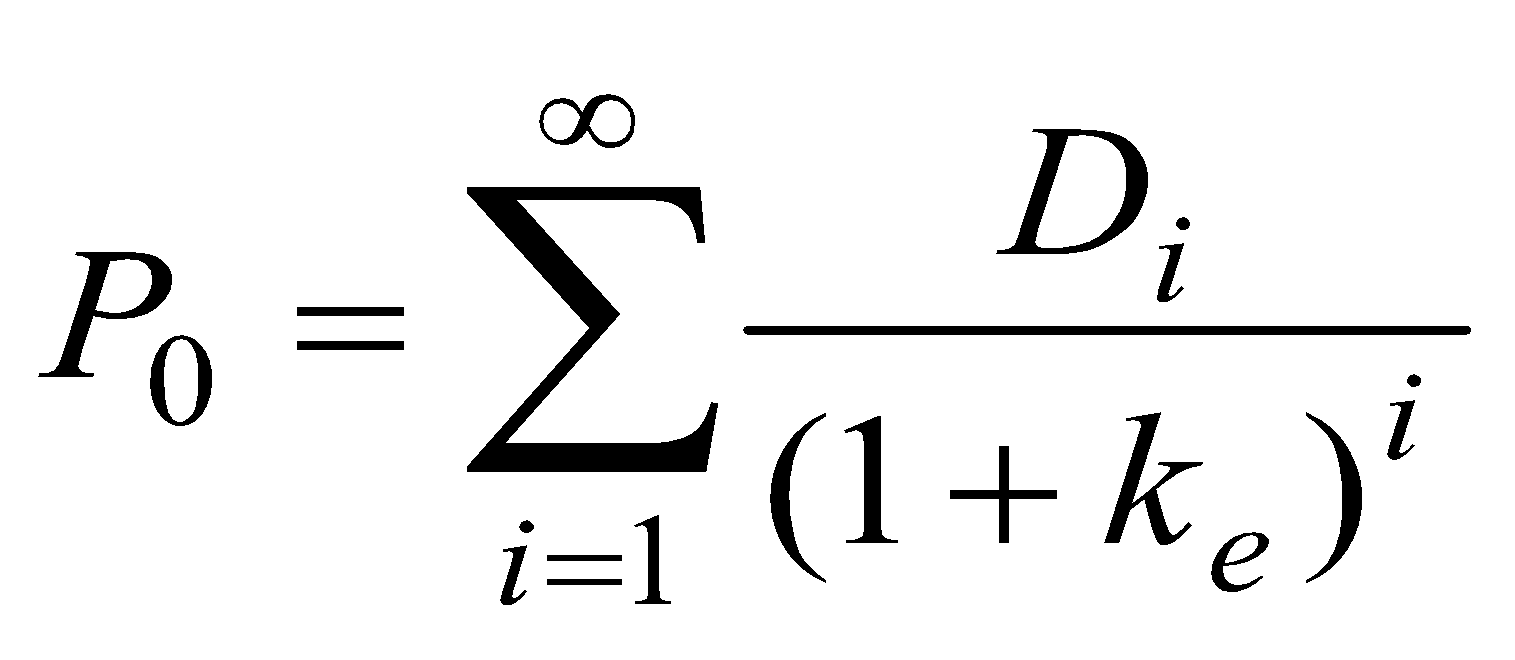
：評價日之評價結果；
：預期第i期發放之現金股利。
另外，設若股利的發放型態是固定成長(包含零成長)，則評價模式可以再簡化為固定成長DDM，即為高登成長模型(Gordon growth model)：
