Table of Contents
造市商具備高頻交易能力、低廉的成本結構與即時的申購/贖回權限,是 ETF 折溢價套利的主要參與者。相較之下,非機構投資人則面臨多重限制,包括資訊延遲與較高的交易摩擦成本(手續費、稅金等),使其難以迅速且獲利地捕捉套利機會。
本篇文章以元大台灣 50(0050 ETF)為例,透過歷史資料模擬這兩種角色在執行折溢價策略中的實際操作,觀察在不同進出場門檻與成本結構下的績效差異。藉由勝率、報酬分布與回撤風險等指標,我們希望釐清:這場「看似無風險的套利」,究竟誰能真正掌握機會,並在台灣市場中賺取穩定的超額報酬(Alpha)?
本實證分析納入了台灣資本市場特有的下列結構性特徵:
優惠稅制: ETF 的證券交易稅享有顯著的政策誘因,稅率僅為 0.1%,遠低於個股交易徵收的 0.3%。
實物申購/贖回: 0050 ETF 主要採用「實物」機制,使法人參與者能利用一籃子股票,在初級市場與次級市場之間進行套利交易。
交割週期: 交易遵循 T+2 交割協議。
資產管理規模 (AUM): 截至 2025 年 1 月,其 AUM 約為 4,400 億新台幣,持續穩坐台灣市場最具流動性且最具基準代表性的 ETF 地位。
追蹤指數: 臺灣證券交易所台灣 50 指數(由市值前 50 大的公司組成)。
本研究之量化數據取自 TEJ 資料庫。透過標準化之公司資本形成資訊處理與歷史價格還原(包含除權息調整),TEJ 得以確保跨期間資料之一致性,進而為本研究之實證分析提供穩健且可靠的基礎。
訊號標準化
本策略採用以下定義之折溢價率作為核心指標,而非採用絕對價差。
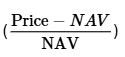
此方法能將訊號標準化,確保在該 ETF 橫跨十年的價格成長過程中(從約新台幣 50 元上漲至超過 150 元),模型對波動性的敏感度能保持一致。
參數穩健性
為了嚴格消除前瞻偏差,本模型採用靜態參數法:
執行邏輯(標準差門檻)
本策略在折溢價率顯著偏離歷史均值時,利用其均值回歸特性進行獲利。針對不同的成本結構,研究測試了兩種門檻:
報酬歸因方法論
為了分離出超額報酬(Alpha)的來源,本策略將報酬分解為以下兩個組成部分:
透過這種分解方式,我們可以驗證獲利究竟是源於基本面價值的調整(淨值),還是由流動性驅動的價格修正(市場價格)。
圖 1:元大台灣 50 (0050) 之長期價格走勢與折溢價結構圖
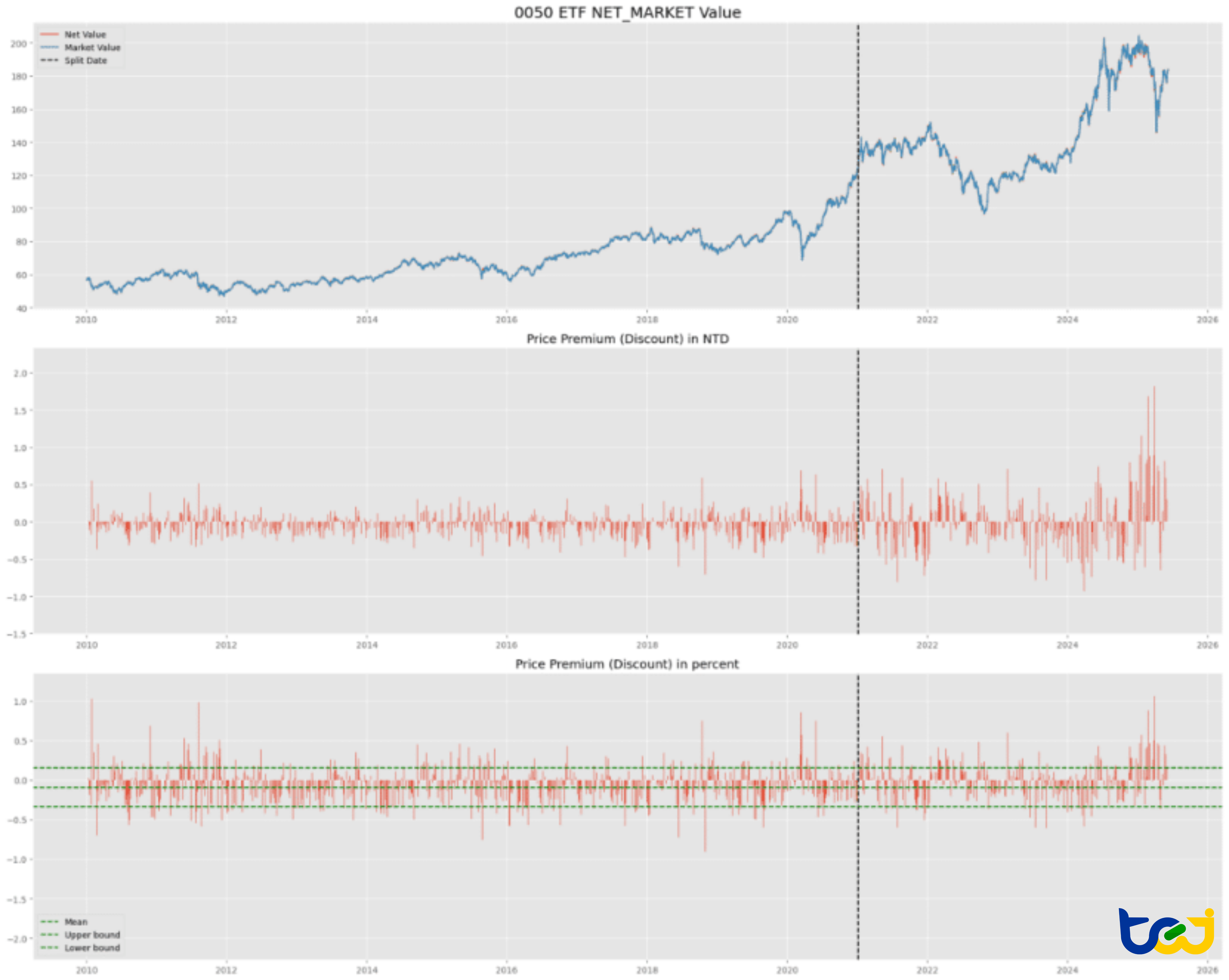
造市商受益於證券交易稅的豁免以及手續費減免,能夠有效地利用微小的偏離(±1σ)來獲利。
圖 2:造市商策略績效表現(1 倍標準差門檻)
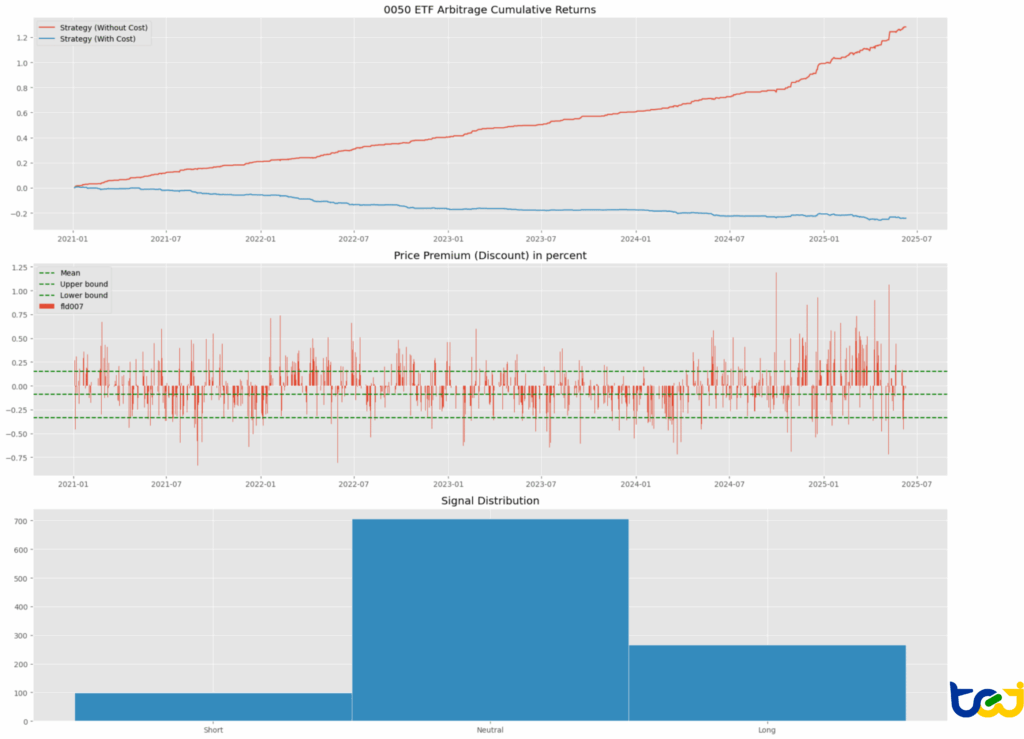
無摩擦超額報酬:如上圖(紅線)所示,造市商接近零成本的交易產生了穩定的正報酬。這證實了 0050 ETF 存在大量短期的均值回歸機會。
成本壁壘:藍線展示了一種反事實情境:如果將標準交易成本套用於此高頻的 1 倍標準差(1-SD)策略,累計報酬將呈線性下滑。這證明了此區域的「超額報酬」具有結構性特徵——它專屬於具備造市特權的參與者。
透過分解利潤來源,揭示了此套利機制的運作原理:
圖 3:報酬歸因分析(淨值 vs. 市場價格)
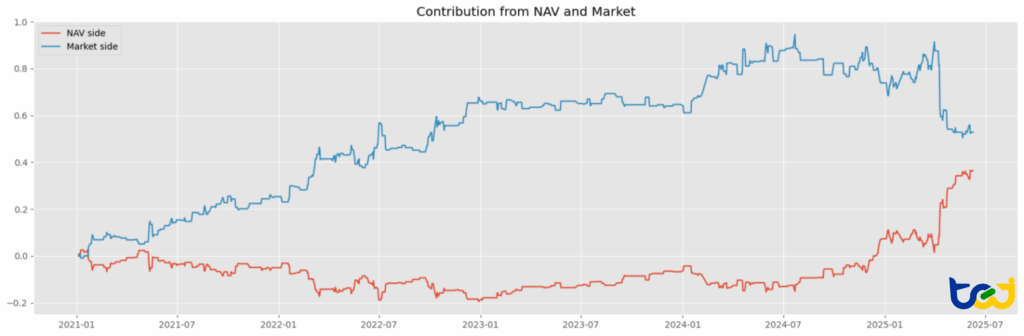
市場價格主導性:大部分的獲利(多頭市值 / 空頭市值)皆源自於 ETF 的市場價格向其公平價值收斂。
淨值端的滯後性:淨值端的貢獻微乎其微、甚至為負值。這與市場微觀結構理論相符:ETF 價格會對流動性衝擊與市場情緒做出反應(進而產生價差),而一籃子成分股(NAV)則保持相對穩定。套利利潤來自於「修正市場價格的無效率」,而非「預測淨值的走動」。
對於非機構參與者而言,該策略必須將進場門檻收緊至 3 倍標準差(3-SD),以作為抵銷 0.1% 證券交易稅與交易手續費的緩衝空間。
圖 4:非機構參與者策略績效表現(3 倍標準差門檻)
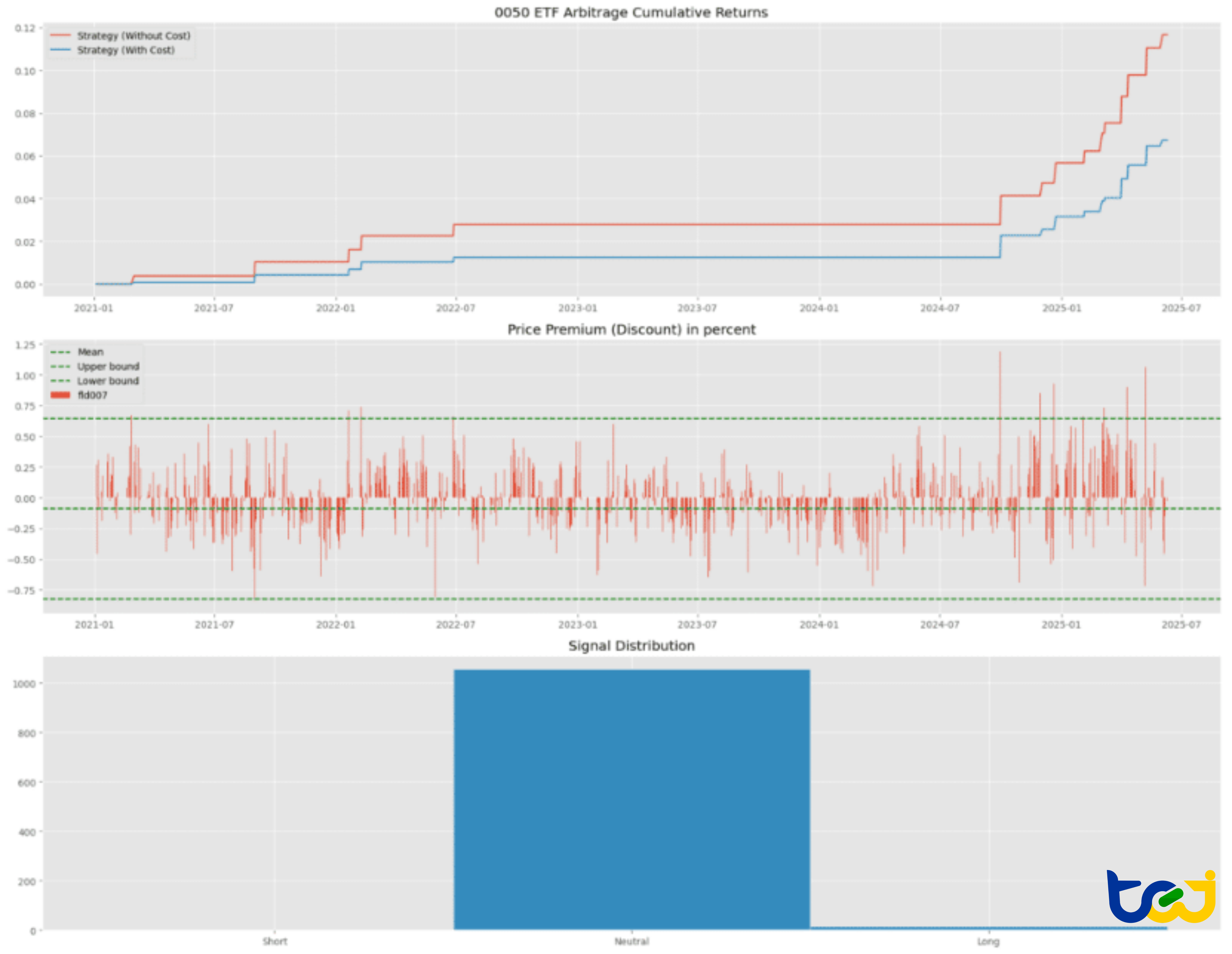
機會稀缺性: 如圖所示,嚴格的 3 倍標準差(3-SD)門檻過濾掉了絕大多數的交易訊號。在長期的觀測中,交易活動呈現顯著的「沉寂期」,有效的訊號高度集中在 2024 年 7 月之後。
報酬侵蝕:
資金效率分析: 雖然單筆交易的「勝率」很高,但資金利用率卻極低。對於機構配置者而言,在此特定期間內為了 7% 的總報酬而鎖定資金,且伴隨長期的閒置期,與風險偏低的債券或簡單的「買入並持有」策略相比,這顯然並非資金的最佳配置。
為了綜合上述實證結果,下表對比了兩類參與者在結構性與營運層面上的分歧:
| 評估指標 | 造市商 (1-SD) | 非機構參與者 (3-SD) |
|---|---|---|
| 主要優勢 | 稅收與費用豁免 | 無(標準交易成本) |
| 交易邏輯 | 高頻流動性提供 | 機會主義 / 狙擊手模式 |
| 交易頻率 | 高(持續性交易) | 極低(稀疏且零星) |
| 勝率 | 高 | 100%(於觀測樣本區間內) |
| 獲利來源 | 交易量 × 微小價差 | 偶發的極端定價錯誤 |
| 資金效率 | 高(持續周轉) | 低(資金長期處於閒置狀態) |
| 策略可行性 | 核心策略 | 低效率(存在更佳的替代方案) |
從台灣市場最具代表性的ETF- 0050實證數據證實,ETF 折溢價套利並非一項「平民化」的策略。
對造市商而言,這代表了一種穩定且高機率的收入流,其獲利源自於提供流動性以及制度性的稅收優勢。
對非機構投資者而言, 該策略表現出明顯的「負不對稱性」。台灣的交易成本——特別是買賣價差與證券交易稅——有效地阻隔了絕大多數的套利利潤。
除非發生極罕見的極端價格錯位,或是具備次分鐘級別的盤中執行能力,否則對於非機構參與者來說,標準的收盤均值回歸方法所提供的風險調整後報酬顯然不足。
綜合本文實證結果可以發現,ETF 折溢價套利並非單純的交易技巧問題,而是高度依賴制度條件、交易成本與執行能力的結構性策略。要客觀驗證這類策略是否具備長期可行性,關鍵不在於單一回測結果,而在於是否使用「當時市場真正可得的資訊」,並在回測中完整納入稅負、手續費與滑價等現實摩擦。這正是量化研究中最容易被忽略、卻也最影響結論可信度的核心環節。
在量化研究與策略驗證過程中,高品質資料與專業工具扮演關鍵角色:
透過 TEJ 量化資料庫與 TQuant Lab 回測系統,研究者得以在貼近市場實務的條件下,深入檢驗 ETF 策略背後的制度性差異與風險結構。無論是重現經典投資策略,或進一步探索市場微結構所帶來的長期影響,TEJ 都能協助您以高品質資訊為起點,建立更具實證基礎與可重複驗證的量化研究流程。
本文內容僅供研究與學術探討之用,不構成任何投資建議。