
Table of Contents
在連續兩周較為複雜的內容之後,讓我們休息一下,回到兩周以前重點【資料科學練功坊】,把基礎資料處裡分析當中的最後一樣重要的工具–資料視覺化進行一個簡單的介紹以及應用吧!!如果忘記之前的內容,可以回去複習一下再回來噢~~
Python能夠用來做資料視覺化的package其實非常多,除了我們今天要介紹的之外,還有像是seaborn, plotly, cufflinks等等,但其實語法還有架構上都大同小異,但因為matplotlib的歷史最為悠久,以及它跟pandas的連接較為緊密,所以我們本篇主要透過它進行教學,如果讀者看過之後對其他的package有興趣可以再自行研究~~
想了解全部內容可以透過連結進入官方document:matplotlib
操作步驟在不同的圖表製作上會有一點點的不同,但使用起來其實非常相似,都是將資料整理好之後,投入該package的函式,然後設定圖表的細項設定,最後就是繪出圖表,說起來可能有點抽象,那就讓我們一步一步來吧!
我們首先將台積電(2330)跟聯電(2303)的股價資料從TEJ API上抓下來。
import tejapi tejapi.ApiConfig.api_key = "your key"
TSMC = tejapi.get(
'TWN/EWPRCD',
coid = '2330',
mdate={'gte':'2020-06-01', 'lte':'2021-04-12'},
opts={'columns': ['mdate','open_d','high_d','low_d','close_d', 'volume']},
paginate=True
)
UMC = tejapi.get(
'TWN/EWPRCD',
coid = '2303',
mdate={'gte':'2020-06-01', 'lte':'2021-04-12'},
opts={'columns': ['mdate','open_d','high_d','low_d','close_d', 'volume']},
paginate=True
)
UMC = UMC.set_index('mdate')
TSMC = TSMC.set_index('mdate')
TSMC['5_MA'] = TSMC['close_d'].rolling(5).mean()
plt.figure(figsize = (10, 6))
plt.plot(TSMC['close_d'], lw=1.5, label = 'Stock Price')
plt.plot(TSMC['5_MA'], lw=1.5, label = '5-Day MA')
plt.legend(loc = 0)
plt.xlabel('Date')
plt.ylabel('Stock Price')
plt.title('TSMC Stock Price vs 5-Day MA')
plt.grid() plt.show()
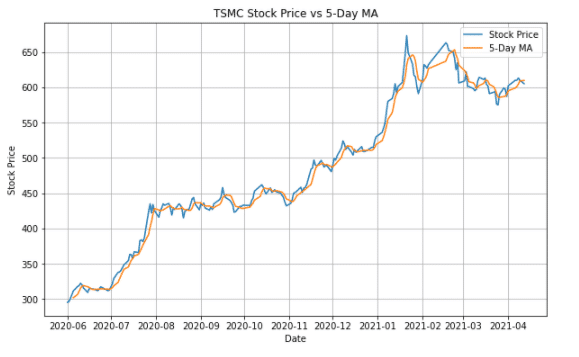
作圖方式大部分都差不多,因此這邊先將最常使用的幾個函式做介紹,會了之後一通百通,在接下來的應用上就只會將不同之處點出來囉~
plt.plot(): 數據帶入後作圖,其中可以設定像線的寬度、顏色、名稱等等
plt.figure(figsize = (10,6)): 設定圖的大小
plt.legend(): 圖例放在甚麼地方(loc=0表示最佳位置)
plt.grid(): 增加網格
plt.xlabel(): X軸名稱
plt.ylabel(): Y軸名稱
plt.title(): 表頭名稱
fig, ax1 = plt.subplots(figsize=(10,8))
plt.plot(TSMC['close_d'], lw=1.5, label = '2330.TW')
plt.xlabel('Date')
plt.ylabel('Stock Price')
plt.title('TSMC VS UMC Stock Price')
plt.legend(loc=1)
ax2 = ax1.twinx()
plt.plot(UMC['close_d'], lw=1.5, color = "r",label = '2303.TW')
plt.ylabel('Stock Price')
plt.legend(loc=2)
plt.show()
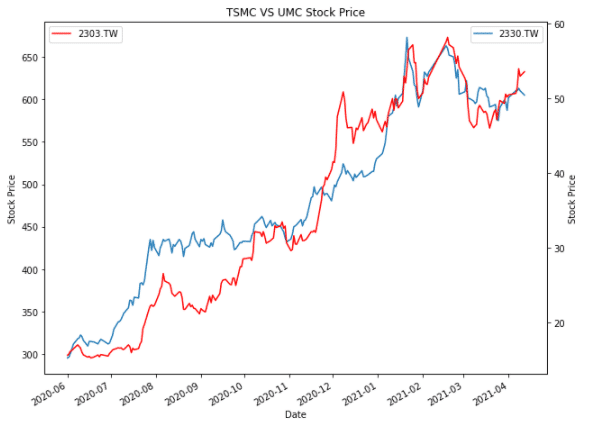
在作圖當中,其實常常會有雙軸圖的需求,因為不同單位或者量級如果將其放在同一個軸的話可能判讀上並不是這麼方便。
那在這之中的做法主要就是透過
fig, ax1 = plt.subplots() 跟
ax2 = ax1.twinx()
去產生第二個圖表但是跟第一個圖表的X軸共用,所以可以理解成做了兩個X軸一模一樣單位的圖片然後再把他們疊起來的意思!
接下來介紹一些非折線圖但是也是常常會被使用的圖表,其實做法都差不多,就是看使用者對於當前資料集想要從甚麼角度去分析而因此做不同的圖表噢!
##散點圖 from sklearn.linear_model import LinearRegression
plt.figure(figsize = (10, 6)) plt.scatter(TSMC['close_d'], UMC['close_d'], color = 'navy')
##回歸線繪製 reg = LinearRegression().fit(np.array(TSMC['close_d'].tolist()).reshape(-1,1), UMC['close_d']) pred = reg.predict(np.array(TSMC['close_d'].tolist()).reshape(-1,1)) plt.plot(TSMC['close_d'], pred, linewidth = 2, color = 'r',label = '迴歸線')
plt.xlabel('TSMC')
plt.ylabel('UMC')
plt.title('TSMC vs UMC')
plt.show()
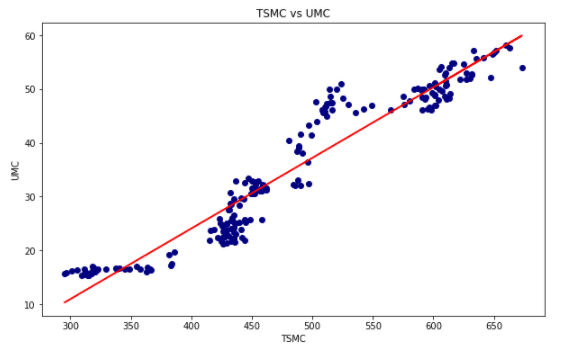
首先介紹散點圖,散點圖可以看出兩資料間的關係,若再搭配上我們回歸線的應用就可以看出兩資料間的相關性~所以在這邊主是要用plt.scatter()跟回歸線製作的方式將這個圖跟線分別做出。
##直方圖 ret_tsmc = np.log(TSMC['close_d']/TSMC['close_d'].shift(1)).tolist()
plt.figure(figsize = (10, 6)) plt.hist(ret_tsmc, bins = 25)
plt.xlabel('Log Return')
plt.ylabel('Frequency')
plt.title('Log Return vs Frequency')
plt.show()
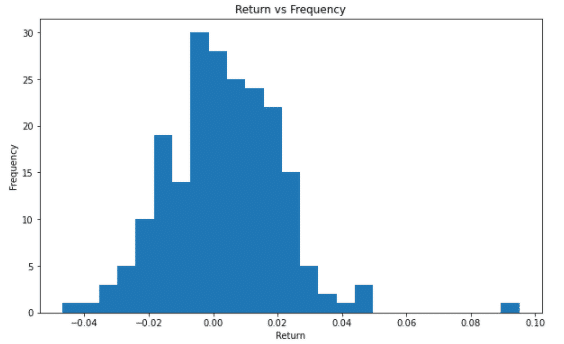
再來則是直方圖,我們可以用直方圖的方式去了解說像是整年度的對數報酬率出要分布在甚麼區間以及他們的出現頻率為何。那直方圖主要差異就是用plt.hist()的方式,並搭配bins去決定說每一個長條之間分隔點為多少(類似決定說寬度是多少)。
##箱型圖 rv = np.random.standard_normal((1000,2))
plt.figure(figsize = (10, 6)) plt.boxplot(rv)
plt.xlabel('dataset')
plt.ylabel('value')
plt.title('ramdon variable box plot')
plt.show()
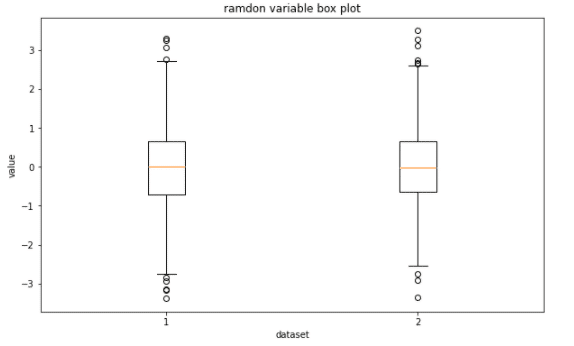
最後就是箱型圖,類似直方圖般一樣可以用來展示資料集的統計特性,並可以一次性的比較很多個資料集。那這邊我們做了一點不一樣的事情是透過生成隨機變數的方式,產出隨機的資料,這不論是在手邊沒有資料或是要透過統計方式生成特定分配的資料型態時都可以用的方法,給大家參考~
在講解完基本的作圖之後,我們接下來就是試著將這些圖表功能應用到財務資料中吧❗️️️️ ❗️️️️
tickers = ['2330', '1301', '2317', '2454' , '2882']
df = tejapi.get(
'TWN/EWPRCD',
coid = tickers,
mdate={'gte':'2020-06-01', 'lte':'2021-04-12'},
opts={'columns': ['mdate', 'coid','close_d']},
paginate=True
)
df = df.sort_values(['coid', 'mdate']).set_index('mdate')
data = df.pivot_table(index = df.index, columns = 'coid', values = 'close_d')
data
data.describe()
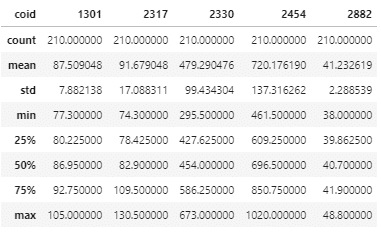
我們可以透過pandas用一行指令的方式就將該標的的敘述統計值給呈現,這其實在資料處裡第一步是一個很一目了然的方式~
##平均報酬率 data.pct_change().mean().plot(kind = 'bar', figsize=(10,6))
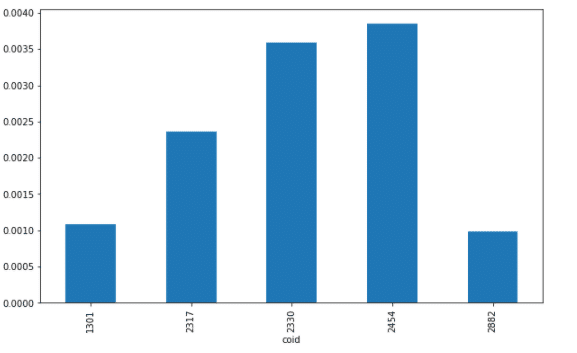
可以看到說,直接透過pandas的特性,將資料變成我們想要的樣子之後,加一個plot(),就可以直接將圖片呈現,是不是非常方便呢?
##累積對數報酬率 ret = np.log(data/data.shift(1)) ret.cumsum().apply(np.exp).plot(figsize = (10,6))
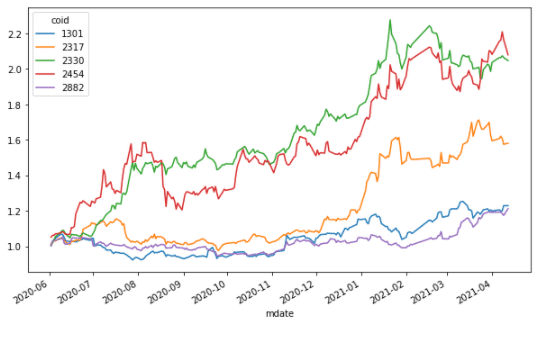
在計算上,主要是透過log的特性,因為log(A)+log(B) = log(AB)這樣的原因,透過連續相加(也就是我們的cumsum)後就會得到最後一項跟第一項相除,再用exp的方式將log消去之後就可以得到我們的報酬率拉~
而在操作上,這邊我們就是透過dataframe+apply的方式對已經取log後的資料先做cumsum()之後再對結果執行np.exp(),進而找出累積對數報酬率~
##最高值/最低值/平均值 windows = 20 data['min'] = data['2330'].rolling(windows).min() data['mean'] = data['2330'].rolling(windows).mean() data['max'] = data['2330'].rolling(windows).max()
ax = data[['min', 'mean', 'max']].plot(figsize = (10, 6), style=['g--', 'r--', 'g--'], lw=1.2) data['2330'].plot(ax=ax, lw=2.5)
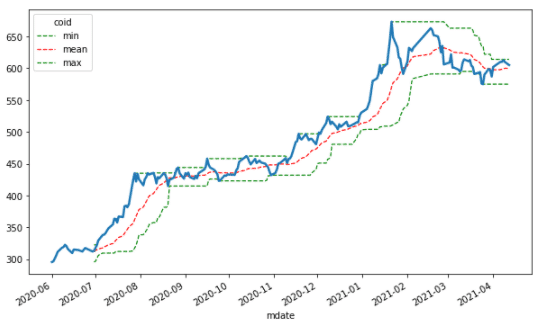
這邊我們也是運用相同的概念,透過pandas將標的物的最高價、最低價、均價都找出來後,然後透過style = [‘g- -‘]的方式去標示顏色還有線條呈現模式後,做出一個上下區間還有均價的圖。
##技術分析-長短天期移動平均線 ##黃金交叉買入/死亡交叉賣出
data['SMA_5'] = data['2330'].rolling(window = 5).mean() data['SMA_20'] = data['2330'].rolling(window = 20).mean()
data[['2330', 'SMA_5', 'SMA_20']].plot(figsize = (10,6))
ata.dropna(inplace = True) data['Positions'] = np.where(data['SMA_5'] > data['SMA_20'], 1, -1)
ax = data[['2330', 'SMA_5', 'SMA_20', 'Positions']].plot(figsize = (10, 6), secondary_y = 'Positions')
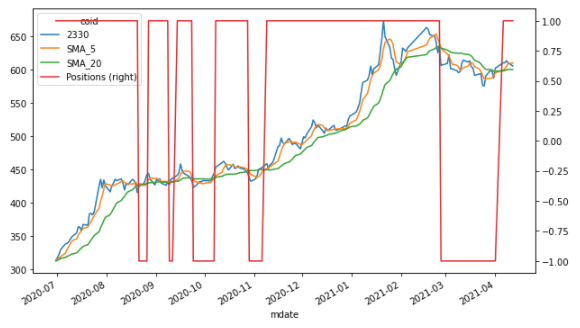
最後就搭配一點技術分析的運用,我們一樣找出長短天期移動平均線後,透過np.where()的方式找到黃金/死亡交叉的位置,並將這些資料透過雙軸圖的方式繪出,因此可以看到說在Position從1到-1的時候就是信號點產生的時候。
圖表製作方法以及呈現方式可以說是百百種,我們在這邊只能夠將最多人使用或者是該種製圖的最基本方式介紹給各位,如果大家對作圖有著很高的興趣,可以多透過這些 package 的官方網站去探索,接下來的文章當中我們也是會持續使用這些作圖方式,並在適合的情況下去做一些額外的變化給各位,請大家好好期待 ❗️❗️
最後,如果喜歡本篇文章的內容請幫我們點擊下方圖示 ,給予我們更多支持與鼓勵,有任何的問題都歡迎在下方留言/來信,我們會盡快回覆大家
有任何使用上的問題都歡迎與我們聯繫:聯絡資訊