
Table of Contents
投資一定會伴隨著風險,然而並不是所有風險都是無可必免的,每個人心裡都不免會有「損失厭惡」的情節產生,透過分散投資,將資金分散在不同的市場之中,由於資產類別的不同,投資人可以有效管理風險,並減低市場波動對投資組合的影響,本篇文章將主要探討如何使用數據,以客觀科學的角度比較基金之間的相似程度。
本文使用 MacOS 作業系統以及 Jupyter Notebook 作為編輯器
# 載入所需套件
import pandas as pd
import re
import numpy as np
import tejapi
import plotly.graph_objects as go
import random
import seaborn as sns
import math
# 登入TEJ API
api_key = 'YOUR_KEY'
tejapi.ApiConfig.api_key = api_key
tejapi.ApiConfig.ignoretz = Truefund = tejapi.get('TWN/AATT',
paginate = True,
opts = {
'columns':['coid', 'mdate', 'isin',
'fld006_c', 'fld007_c',
'fld014_c','fld015',
'fld016_c','un_name_c',
'risk', 'main_flag',
'fld021', 'currency', 'aunit1',
]
}
)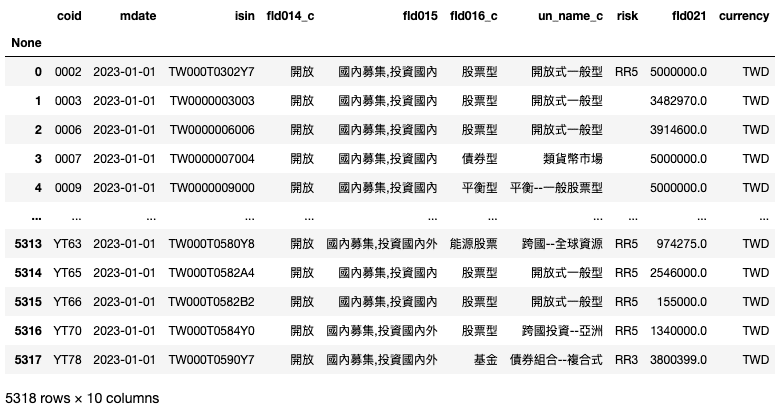
本次實作所需要的欄位有:
由於大多數欄位為文字資料,因此在資料預處理時要先將其轉換為序數,一般這樣的做法可以直寫使用ordinal encoding的相關套件,但由於投資標的的類型間存在著風險大小的關係,因此本次實作就自行定義各類別的相應序數,以確保之間的相對風險關係正確。
為了給予序數,我們將資料表內投資標的的所有類別打印出來
fund["fld016_c"].unique()
style = {
'':0,
'保本型': 1,
'貨幣型': 2,
'債券型': 3,
'平衡型': 4,
'ETF': 5,
'指數型基金': 6,
'基金': 7,
'多重資產': 8,
'股票型': 9,
'房地產': 10,
'產證券化': 11,
'不動產證券化': 12,
'科技股': 13,
'小型股資': 14,
'能源股票': 15,
'期貨商品': 16,
}
risk = {
"":0,
"RR1":1,
"RR2":2,
"RR3":3,
"RR4":4,
"RR5":5,
}
area = {
"國內募集,投資國內":1,
"國內募集,投資國內外":2,
"國外募集,投資國內":3,
}
OorC = {
"封閉":0,
"開放":1,
}
# adjust sting data to Ordinal encoding data
fund_adj = fund.copy()
fund_adj["fld015"] = fund_adj["fld015"].apply(lambda x: area.get(x))
fund_adj["fld016_c"] = fund_adj["fld016_c"].apply(lambda x: style.get(x))
fund_adj["risk"] = fund_adj["risk"].apply(lambda x: risk.get(x))
fund_adj["fld014_c"] = fund_adj["fld014_c"].apply(lambda x: OorC.get(x))再來由於需要使用視覺化圖表呈現基金的相似程度,各數值間需要進行尺度的縮放以符合圖表規格,因此這裡我們對於「成立資產」進行正規化,將數字範圍更改為介於 0 ~ 17 之間( 因為投資標的的最大序數為16 ),經過此處理後「成立資產」僅能呈現不同基金成立金額間的比例差距,不再具有真實的金額意義。
# min-max normalization
size = np.array(fund_adj["fld021"].fillna(0))
size = (size - size.min()) / (size.max() - size.min())*len(style)
fund_adj["fld021"] = size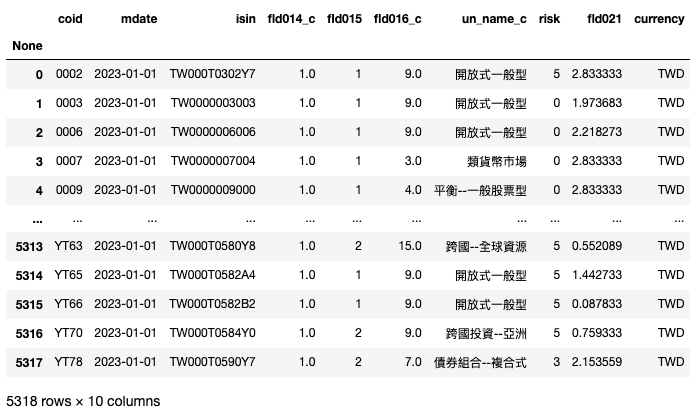
我們篩選幣別為新台幣的基金進行視覺化圖表呈現,本次將以雷達圖呈現基金之間的差異程度,我們隨機在資料集中抽取 10 檔基金來進行相似度比較。
fund = fund[fund["currency"].str.contains("TWD")]
# randomly pick 10 funds
# set the random state
isin_lst = list(fund["isin"].unique())
random.seed(1)
random_isin_lst = random.sample(isin_lst, 10, )
check_lst = random_isin_lst
categories = ['開放型基金/封閉型基金','募集地及投資區域','投資標的',
'風險', '成立資產']
fig = go.Figure()
data_lst = []
for num, isin in enumerate(check_lst):
data = list(fund_adj[fund_adj["isin"] == isin][["fld014_c", "fld015", "fld016_c", "risk", "fld021"]].iloc[0, :])
data_lst.append(data)
fig.add_trace(go.Scatterpolar(
r=data,
theta=categories,
fill='toself',
name=isin
))
fig.update_layout(
polar=dict(
radialaxis=dict(
visible=True,
range=[0, len(style)]
)),
showlegend=True
)
fig.show()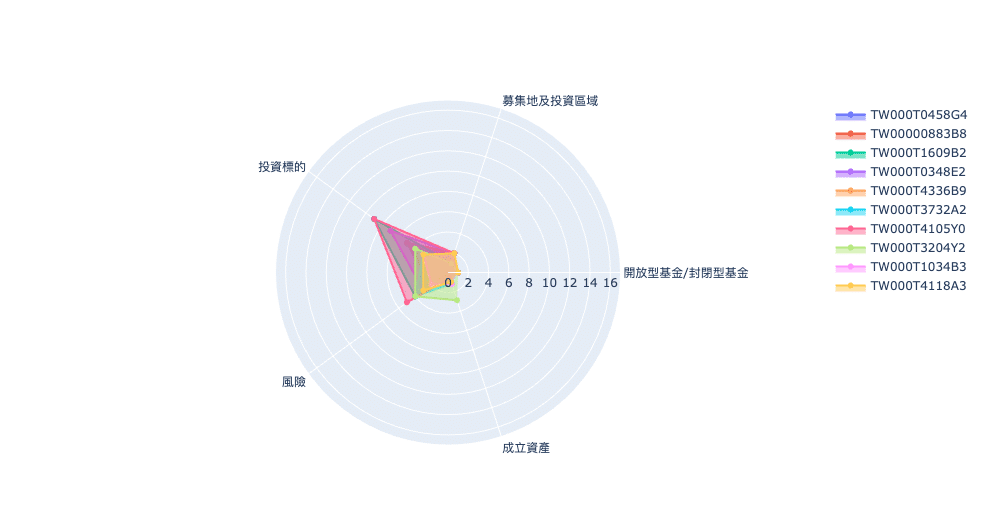
雷達圖可以清晰快速的幫助我們了解各基金項目之間差別,然而它卻無法給予我們一個具體的數值關於到底兩檔基金之間有多相似,因此接下來將使用餘弦相似度 與 歐式距離 來解決上述問題。
全稱為歐幾里德距離 (Euclidean distance),是一種常見的距離度量方法,用於計算多維空間中任意兩點的直線距離,接下來我們透過程式建立出歐式距離的相關矩陣。
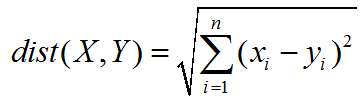
# calculate Euclidean Distance of each couple funds
ED_matrix = np.empty(shape=[len(random_isin_lst), len(random_isin_lst)])
for i in range(len(data_lst)):
for j in range(len(data_lst)):
dist = math.dist(data_lst[i], data_lst[j])
ED_matrix[i, j] = round(dist,5)
print(ED_matrix)
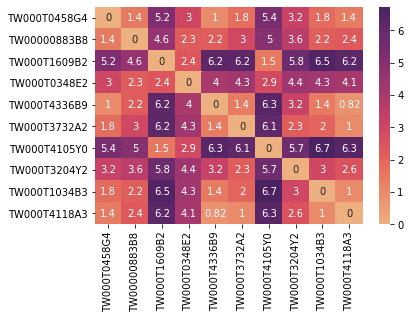
sns.heatmap(ED_matrix, xticklabels = random_isin_lst, yticklabels = random_isin_lst, annot=True, cmap = "flare")如此,我們已經完成歐式距離的計算,但其以矩陣形式呈現的結果非常不好判讀,因此我們再使用另一種視覺化圖表-熱力圖來顯示結果

在歐式距離之中,在未將數據標準化或正規化的情況下,數值並沒有上限,0 代表完全相同,而數值越大代表著兩元素間的距離越遠,也就是差異越大。而在熱力圖中,橫軸與縱軸為基金的ISIN code ,而左上至右下的斜對角代表對應到的元素皆為自己,因此距離永遠為 0 。
餘弦相似度 (Cosine Similarity)通過測量兩個向量的夾角的餘弦值來衡量之間的相似性。 0 度角的餘弦值是 1,代表完全相同,而其他任何角度的餘弦值都不大於 1;並且其最小值是 -1。 從而兩個向量之間的角度的餘弦值確定兩個向量是否大致指向相同的方向。
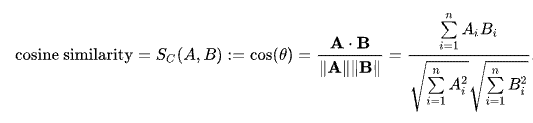
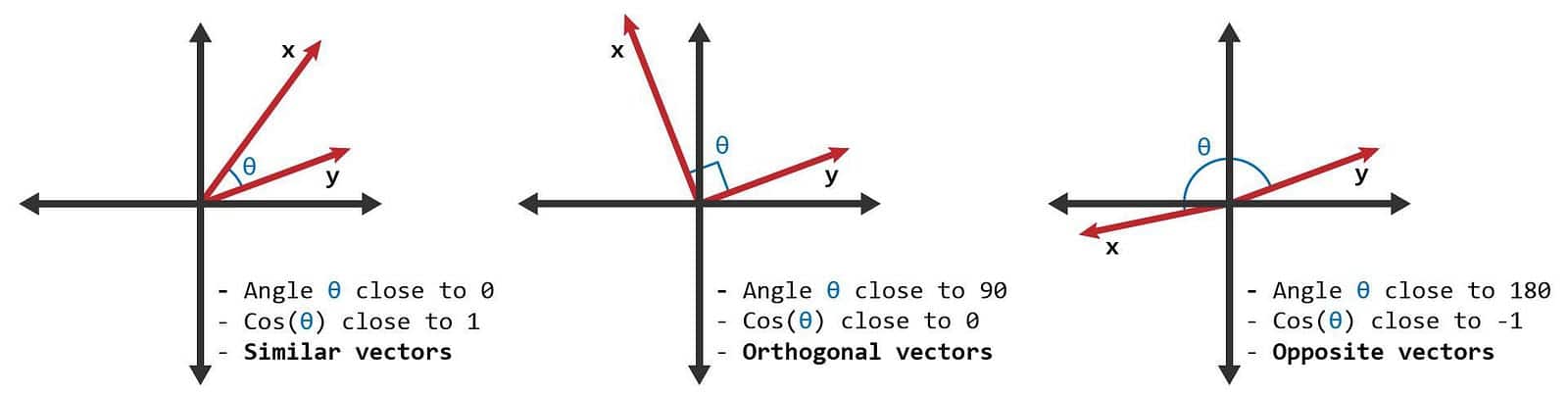
接著我們將公式程式化,作法與計算歐式距離類似,值得注意的是,餘弦相似度不會因為向量的大小而有差異,這是由於餘弦相似度的計算過程中恰好做了類似正規化的處理。
# The measure of cosine similarity will not be affected by the size of the vector
CS_matrix = np.empty(shape=[len(random_isin_lst), len(random_isin_lst)])
for i in range(len(data_lst)):
for j in range(len(data_lst)):
A = np.array(data_lst[i])
B = np.array(data_lst[j])
cosine = np.dot(A,B)/(norm(A)*norm(B))
CS_matrix[i, j] = round(cosine,5)
print(CS_matrix)
sns.heatmap(CS_matrix, xticklabels = random_isin_lst, yticklabels = random_isin_lst, annot=True, cmap = "flare_r")查看餘弦相似度相關矩陣

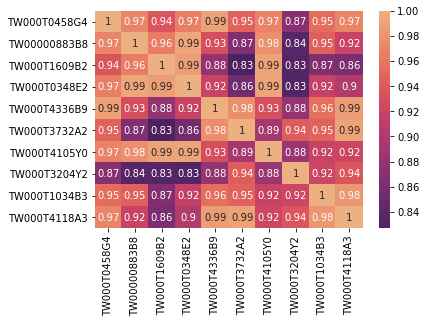
此時眼尖的朋友應該有注意到,歐式距離是數值越小越相似,而餘弦相似度則是數值越大越相似,兩者呈現反關係,因此在熱力圖呈現時應該要講圖表顏色倒轉才比較方便比較兩種計算結果,因此在歐式距離視覺化程式碼中的 cmap = “flare” 在這裡要改為 cmap = “flare_r”。
比較兩張圖,大致上的分布趨勢都相應符合,因為事實上歐式距離就等價於餘弦相似度。
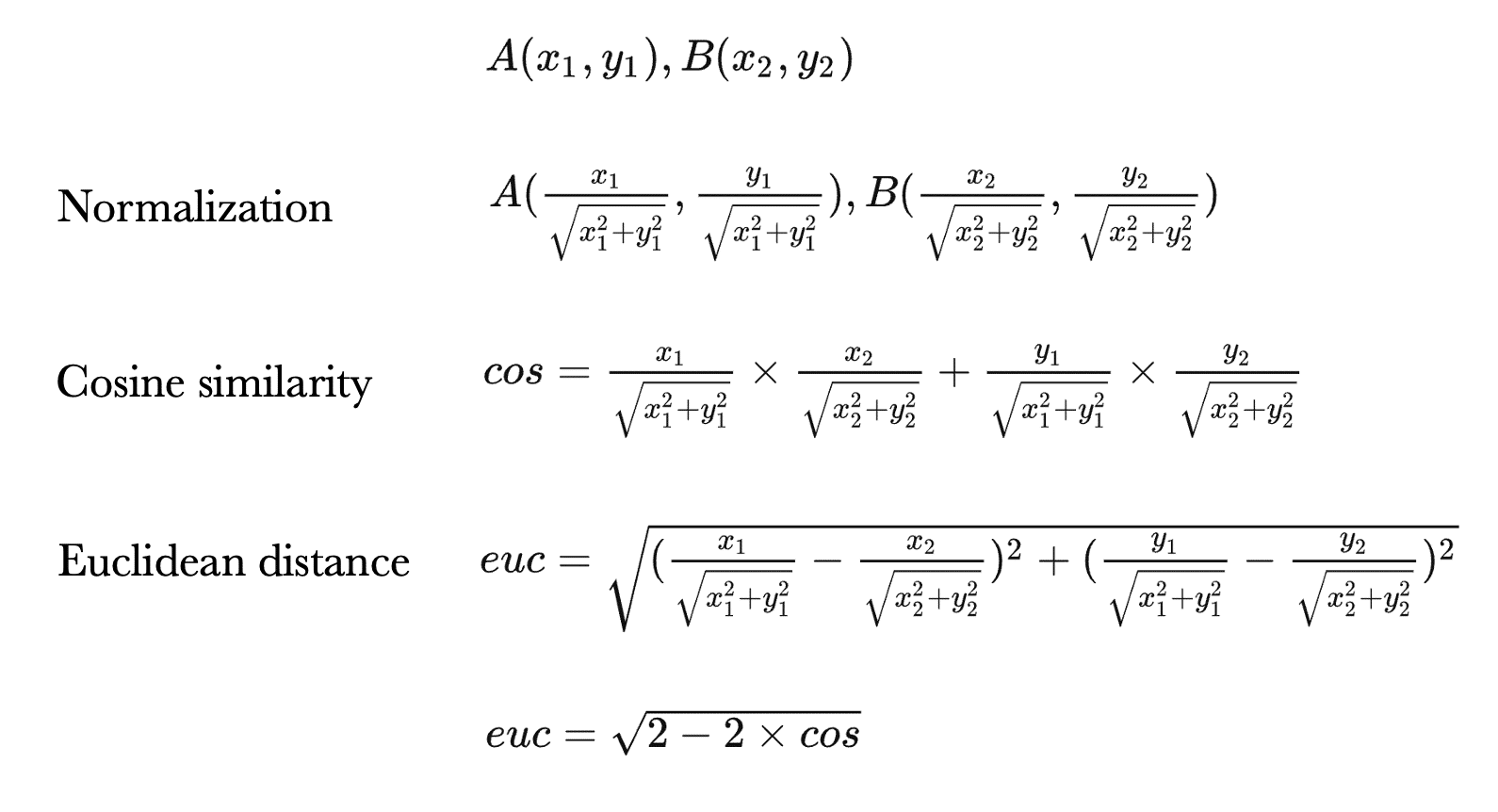
先假設空間中有兩點:A、B
針對 A、B 分別做正規化,所得到的結果即為單位向量
以兩單位向量計算餘弦相似度,其分母為 1 所以在此就直接省略
再以兩單位向量計算其歐式距離,經化簡後即可得證
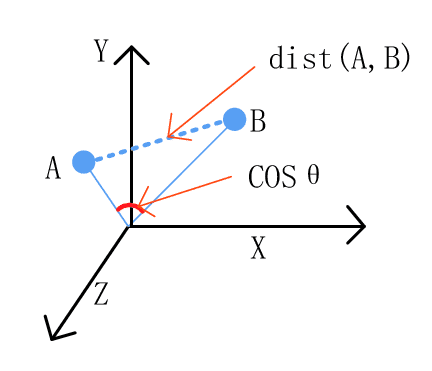
那這樣的話,歐式距離與餘弦相似度的差別到底是什麼呢?
對於歐式距離來說,由於它計算的是兩點之間的直線距離,因此當兩點的趨勢相同,但向量長度不同時,歐式距離就無法反映出這樣的相似性;以本次實作來舉例,當兩檔基金的相似程度極大,只是其中一檔的成立資產較大、另一篇較小時,雖然兩檔基金性質相似,但由於成立資產大小的問題,歐式距離的計算結果仍然會是差距很遠。另一方面,餘弦相似度是計算兩向量的餘弦夾角,因此相似的兩檔基金夾角會很小,因此就可以有效顯示出它們之間的相似性。
在相似度的比較結果上我們可以發現幾乎大多數的境內基金之間相似程度都非常高,這非常有可能是由於本次實作僅僅篩選了基金基本資料的一些資訊,因此僅能反映當初基金成立時的狀態,讀者可以在自行加入其他資訊進行計算,例如報酬率、費用率等等,TEJ API 提供完整的基金資訊以及多種取用方式可讓讀者隨心所欲,客製化自己的比較模組。
溫馨提醒,本次介紹與標的僅供參考,不代表任何商品或投資上的建議。之後也會介紹使用TEJ資料庫來建構各式選擇權模型,所以歡迎對選擇權交易有興趣的讀者,選購TEJ E-Shop的相關方案,用高品質的資料庫,建構出適合自己的訂價模型。