
Table of Contents
霍華.羅斯曼(Howard Rothman)為華爾街知名投資機構「遠見投資顧問公司」(Vision Investment Advisor, VIA)之首席投資分析師,其主導的「藍籌股成長操作帳戶」(Blue Chip Growth Account)自1997年成立以來,至2001年為止累積報酬率高達49.27%,表現為同期標準普爾500指數(S&P500)的兩倍以上,並在各年度中皆穩定優於大盤。
截至2002年12月,羅斯曼已擔任遠見投資顧問公司總裁,並曾擔任國家折扣券商協會(the National Introducing Brokers Association)主席及創始會員。他自1990年起被推薦進入國家期貨協會(the National Futures Association)董事會,連任三屆,並積極參與期貨產業協會的法律與合規委員會,具備深厚的專業背景與業界影響力。
羅斯曼的投資核心理念在於「於正確時機買進並長期持有優質個股」(”buy right and hold tight”、”buy strong and hold long”)。他強調,選擇財務穩健、獲利穩定成長的公司,並於適當價格買入後耐心持有,無須頻繁調整持股,即可獲得長期優異報酬。這種簡潔而堅定的投資哲學,不僅體現出他的實務智慧,也為本次策略回測提供了明確且具有歷史驗證的依據。
本策略核心精神承襲霍華.羅斯曼強調的投資哲學——選擇基本面穩健、具成長潛力的優質公司,並於適當時機進場佈局,長期持有以追求穩定報酬。為此,我們設計一套具體且嚴謹的篩選機制,從全市場中挑選具備穩定獲利能力與成長潛力的個股,條件如下:
透過上述多重條件交叉篩選,我們期望能精準鎖定具備「規模穩健、財務健康、成長動能明確」的企業,建立一組具長期投資價值的股票池,作為後續回測與策略建構的基礎。
通過使用 TQuant 提供的 get_nuiverse 以及 get_histiort_data 函數來獲取需要的股票財務資料,並進行上述篩選標準的計算。
import pandas as pd
import numpy as np
import tejapi
import os
import json
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Arial'
tej_key = 'Your key'
tejapi.ApiConfig.api_key = tej_key
os.environ['TEJAPI_BASE'] = "https://api.tej.com.tw"
os.environ['TEJAPI_KEY'] = tej_key
from zipline.sources.TEJ_Api_Data import get_universe
import TejToolAPI
from zipline.data.run_ingest import simple_ingest
from zipline.api import set_slippage, set_commission, set_benchmark, symbol, record, order_target_percent
from zipline.finance import commission, slippage
from zipline import run_algorithm
start_date = '2010-01-01'; end_date = '2025-04-21'
pool = get_universe(start = start_date,
end = end_date,
mkt_bd_e = ['TSE', 'OTC'],
stktp_e = 'Common Stock',
main_ind_e = 'General Industry')
columns = ['coid','roi', 'mktcap', 'r501', 'r104', 'cscfo', 'cscfi', 'r401', 'r405']
start_dt = pd.Timestamp(start_date, tz = 'UTC')
end_dt = pd.Timestamp(end_date, tz = "UTC")
data_use = TejToolAPI.get_history_data(start = start_dt,
end = end_dt,
ticker = pool,
fin_type = 'Q', # 為單季資料
columns = columns,
transfer_to_chinese = False)
data_use['Avg_Market_Cap_Per_Day'] = data_use.groupby('mdate')['Market_Cap_Dollars'].transform('mean')
data_use['Avg_Current_Ratio_Per_Day'] = data_use.groupby('mdate')['Current_Ratio_Q'].transform('mean')
data_use['Avg_Return_Rate_on_Equity_Per_Day'] = data_use.groupby('mdate')['Return_Rate_on_Equity_A_percent_Q'].transform('mean')
data_use['Free_Cash_Flow'] = data_use['Cash_Flow_from_Operating_Activities_Q'] - data_use['Cash_Flow_from_Investing_Activities_Q']
# 確保資料依公司與時間排序
data_use = data_use.sort_values(['coid', 'mdate'])
# 使用 rolling() 計算近四季平均 ROE(min_periods=4 確保要有滿4筆才計算)
data_use['Avg_ROE_4Q'] = data_use.groupby('coid')['Return_Rate_on_Equity_A_percent_Q'] \
.transform(lambda x: x.rolling(window=252, min_periods=252).mean())
# 使用 rolling() 計算近四季平均營收成長率
data_use['Avg_Sales_Growth_4Q'] = data_use.groupby('coid')['Sales_Growth_Rate_Q'] \
.transform(lambda x: x.rolling(window=252, min_periods=252).mean())
data_use['Avg_NI_Growth_4Q'] = data_use.groupby('coid')['Net_Income_Growth_Rate_Q'] \
.transform(lambda x: x.rolling(window=252, min_periods=252).mean())
# 計算過去1260日(5年)的最小值是否大於0
data_use['FCF_Positive_5Y'] = data_use.groupby('coid')['Free_Cash_Flow'] \
.transform(lambda x: x.rolling(window=1260, min_periods=1260).mean() > 0)
def compute_stock(date, data):
df = data[data['mdate'] == pd.to_datetime(date)].reset_index(drop = True)
set_1 = set(df[df['Market_Cap_Dollars'] >= df['Avg_Market_Cap_Per_Day']]['coid'])
set_2 = set(df[df['Current_Ratio_Q'] >= df['Avg_Current_Ratio_Per_Day']]['coid'])
set_3 = set(df[df['Avg_ROE_4Q'] >= df['Avg_Return_Rate_on_Equity_Per_Day']]['coid'])
set_4 = set(df[df['FCF_Positive_5Y']]['coid'])
set_5 = set(df[(df['Avg_Sales_Growth_4Q'] > 0.06)]['coid'])
set_6 = set(df[(df['Avg_NI_Growth_4Q'] > 0.08)]['coid'])
tickers = list(set_1 & set_2 & set_3 & set_4 & set_5 & set_6)
return tickers
為使投資策略能更貼近真實市場操作,本策略設計以 120 日為一輪的再平衡週期。選擇較長的持有期間主要考量到:企業基本面如營收、盈餘與現金流等財務指標,其變動多數具有一定的滯後性與穩定性,股價需一段時間才能完整反映其內在價值。因此,相較於短期交易策略,採用 120 天(約 6 個交易月)的持有期能更有效捕捉基本面因素對股價的中長期驅動力。
具體流程為:
每 120 個交易日重新進行一次股票池篩選,依據最新財務數據更新篩選結果,並同步汰換不符合標準的個股,納入新符合條件之標的。此作法可兼顧基本面變化與交易成本控制,達成策略穩定性與實務執行的平衡。同時為了確保回測時的槓桿使用是穩健的以貼近真實世界,我們在交易邏輯有另外設計一個槓桿檢查機制,當回測時的槓桿率超過1.2 時,進行股票部位的再調整使其回到 1.0。
pools = pool + ['IR0001']
start_ingest = start_date.replace('-', '')
end_ingest = end_date.replace('-', '')
print(f'開始匯入回測資料')
simple_ingest(name = 'tquant' , tickers = pools , start_date = start_ingest , end_date = end_ingest)
print(f'結束匯入回測資料')
def initialize(context, re = 120):
set_slippage(slippage.VolumeShareSlippage(volume_limit=1, price_impact=0.01))
set_commission(commission.Custom_TW_Commission())
set_benchmark(symbol('IR0001'))
context.i = 0
context.state = False
context.order_tickers = []
context.last_tickers = []
context.rebalance = re
def handle_data_1(context, data):
# 避免前視偏誤,在篩選股票下一交易日下單
if context.state == True:
for i in context.last_tickers:
if i not in context.order_tickers:
order_target_percent(symbol(i), 0)
for i in context.order_tickers:
order_target_percent(symbol(i), 1 / len(context.order_tickers))
curr = data.current(symbol(i), 'price')
record(price = curr, days = context.i)
print(f"下單日期:{data.current_dt.date()}, 擇股股票數量:{len(context.order_tickers)}, Leverage: {context.account.leverage}")
context.last_tickers = context.order_tickers.copy()
context.state = False
backtest_date = data.current_dt.date()
if context.i % context.rebalance == 0:
context.state = True
context.order_tickers = compute_stock(date = backtest_date, data = data_use)
record(Leverage = context.account.leverage)
if context.account.leverage > 1.2:
print(f'{data.current_dt.date()}: Over Leverage, Leverage: {context.account.leverage}')
for i in context.order_tickers:
order_target_percent(symbol(i), 1 / len(context.order_tickers))
context.i += 1
record(ticker_num = len(context.order_tickers))
def analyze(context, perf):
fig, axes = plt.subplots(nrows=3, ncols=1, figsize=(18, 10), sharex=False)
plt.style.use('ggplot')
axes[0].plot(perf.index, perf['algorithm_period_return'], label = 'Strategy')
axes[0].plot(perf.index, perf['benchmark_period_return'], label = 'Benchmark')
axes[0].set_title(f"Backtest_Results")
axes[0].legend()
axes[1].plot(perf.index, perf['Leverage'], label = 'Leverage')
axes[1].set_title(f"Leverage")
axes[1].legend
axes[2].plot(perf.index, perf['ticker_num'], label = 'Ticker_number')
axes[2].set_title(f'Ticker Number')
axes[2].legend()
plt.tight_layout()
plt.show()
results = run_algorithm(
start = pd.Timestamp('2019-01-01', tz = 'utc'),
end = pd.Timestamp(end_date, tz = 'utc'),
initialize = initialize,
handle_data = handle_data_1,
analyze = analyze,
bundle = 'tquant',
capital_base = 1e5)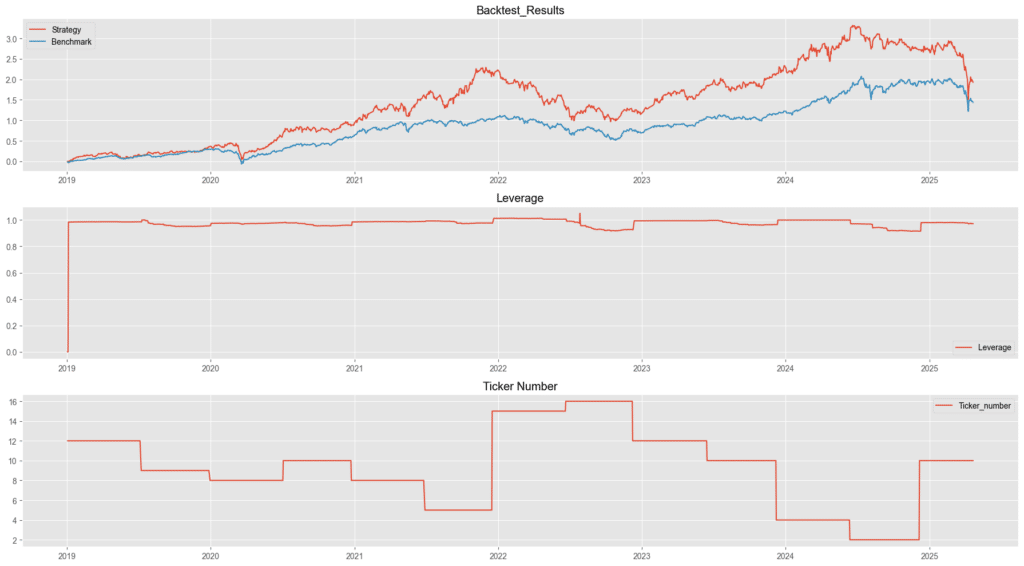
上圖展示了策略的累積報酬率、槓桿使用率以及持倉的股票數量。從槓桿率的線圖來看,策略回測結果並沒有使用到過高的槓桿,也沒有過多的現金儲備造成侵蝕整體報酬率的情況。以投資的股票數量來看,每次篩選股票出的股票數平均是在 10 支股票左右,這顯示出策略的嚴謹程度是中,不會因篩選條件過於嚴格而篩選掉所有股票,同時也不會因篩選條件過於鬆散,而造成下單股票數量過多造成績效貼近大盤。
從累積報酬率的線圖來看,策略跑贏大盤的時機點主要處於 2020年初 – 2022 年初以及 2023 年初 – 2024 5、6月,這兩個時期剛好對應到大盤的主要上漲期間。與此同時在 2022 – 2023 年初的時期以及 2024 年中至今的這兩個時期則是容易輸給大盤的漲幅(兩條線的距離靠近),對應到大盤進入熊市或是盤整格局。因此我們認為此策略是根據價值投資的概念去做選股,因此在牛市時期較容易出現價格反應公司價值的狀況,而熊市時期的情緒面容易影響股票的短期價格,造成價值投資在此時期的效果大大減半。
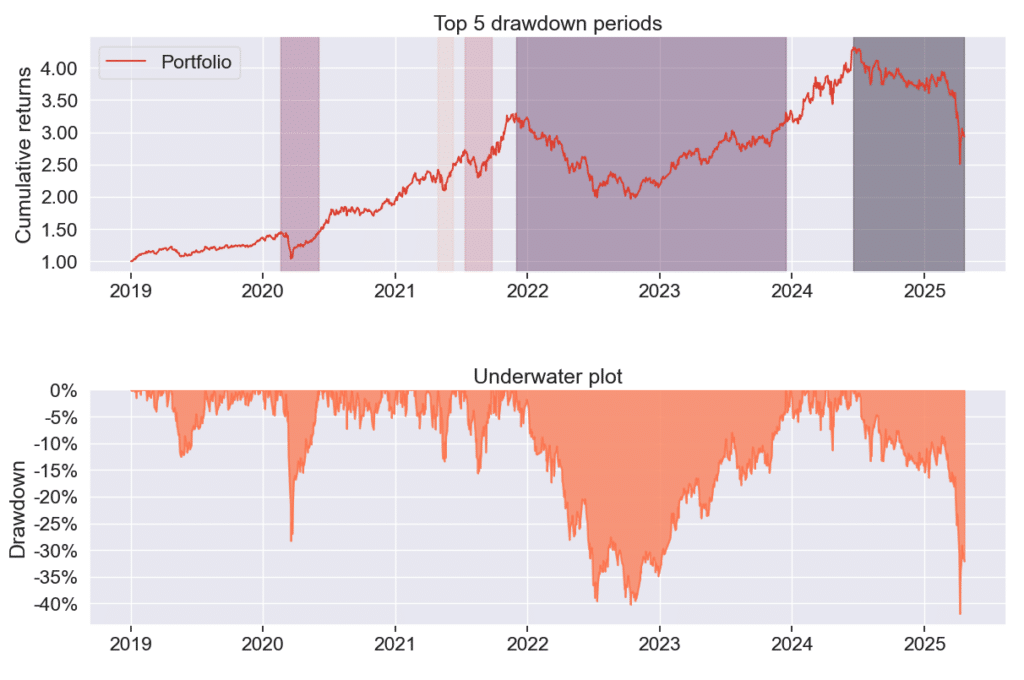
從上圖可以看出 2022 至 2024 年初的期間是整體策略最大的回撤期間,顯示出此策略仰賴整體市場的狀態,而非能夠在不同的市場情況都能夠賺取超額報酬,因此需要視市場情況來盼對是否使用此策略。
| 績效指標 / 策略 | 大盤(Benchmark) | 霍華.羅斯曼投資策略 |
| 年化報酬率 | 14.5% | 19.43% |
| 累積報酬率 | 126.97% | 193% |
| 年化波動度 | 17.08% | 26.43% |
| 夏普值 | 0.88 | 0.8 |
| 卡瑪比率 | 0.55 | 0.46 |
| 期間最大回撤 | – 26.295% | – 41.937% |
在本研究中,將霍華.羅斯曼(Howard Rothman)投資策略與大盤表現進行比較,發現其在報酬能力上具有明顯優勢。該策略的年化報酬率為 19.43%,顯著高於大盤的 14.5%,累積報酬亦高達 193%,優於大盤的 126.97%。然而,其風險指標亦相對較高,年化波動度達 26.43%(大盤為 17.08%),最大回撤亦來到 -41.94%,低於大盤的 -26.30%,主要是篩選條件較嚴導致成分股數較低,使得整體投組分散性不佳。最終也使夏普值略低(0.80 vs 0.88),表示風險調整後的效益未能優於大盤,但整體而言,該策略在絕對報酬表現上仍展現出強勁的潛力。
歡迎投資朋友參考,之後也會持續介紹使用 TEJ 資料庫來建構各式指標,並回測指標績效,所以歡迎對各種交易回測有興趣的讀者,選購 TQuant Lab 的相關方案,用高品質的資料庫,建構出適合自己的交易策略。
溫馨提醒,本次分析僅供參考,不代表任何商品或投資上的建議。