
Table of Contents
在金融市場中,風險與報酬的關係,往往未必如經典理論所描繪般呈現正向線性。實證經驗顯示,低風險資產反而可能取得更佳表現,這類現象被稱為「低波動性異象」。本文以台灣市場為例,探討該異象在台灣市場中的表現與特性,並聚焦於其中一項重要因子:特質波動度(Idiosyncratic Volatility),進一步評估其作為投資工具的可行性與應用價值。
傳統資產定價理論認為,風險越高,預期報酬也應越高。然而,實證研究卻發現,歷史波動度較低的股票,無論在絕對報酬或風險調整後表現上,往往優於高波動股票,形成所謂的低波動性異象(Low-Volatility Anomaly)。早在 1970 年代,Black (1972) 即已注意到,Beta 與實際報酬之間的關係遠比理論預期平緩。
行為財務學對此現象提出多種可能解釋,例如彩券效應(Lottery Effect)、代表性偏誤(Representativeness Bias)與過度自信(Overconfidence Bias)等:投資人偏好高波動、類似彩券的資產,容易為其支付過高溢價,並對未來高成長機會過度樂觀,最終導致高波動股票長期表現不佳(Blitz, Falkenstein, and van Vliet ,2014)。
後續研究進一步驗證,即使控制市場、規模、價值、動能等因子,低波動策略仍能持續產生超額報酬,顯示這一現象具備跨時期與跨市場的穩定性。低波動性異象不僅挑戰了傳統理論,也在 2008 年金融海嘯後因防禦型需求提升而受到市場廣泛關注,推動了 Smart Beta 與因子型 ETF 的興起。
在台灣市場,結合「高股息」與「低波動」概念的 ETF,如國泰股利精選30(00701)、元大台灣高息低波(00713)等產品,亦成為投資人追求穩健報酬的重要選擇。從理論觀察到實務應用,低波動性異象已深刻影響現代資產配置邏輯與市場策略發展。
👉延伸閱讀:TQuant Lab 存股族的福音?高股息 ETF 的回測表現
儘管如此,部分近期學術研究亦指出,低波動策略的超額報酬可能部分來自於對其他風險因子的曝險,而非獨立存在的異象。Novy-Marx (2014) 及 Fama and French (2015) 發現,在納入獲利能力(Profitability)與投資(Investment)等因子後,低波動策略的報酬大多可以被吸收;此外,van Vliet (2012) 與 Garcia-Feijóo, Kochard, Sullivan, and Wang (2015) 亦指出,低波動組合的表現隨市場風格變化而波動,並非恆常穩定。
然而,即便在考慮了各種風格因子與模型後,部分與風險有關的異象仍難以完全納入現有框架解釋。其中最具代表性的,便是特質波動度異象(Idiosyncratic Volatility Puzzle):一種不同以往的波動度指標,其異常表現長期以來持續挑戰著傳統資產定價理論。
Factor Library因子資料庫 – 涵蓋動能、股息率、價值、成長等九大因子分類,高效率實踐因子投資
除了投資理論中常被提及的系統性風險外,個別資產的特有風險在資產報酬行為中的角色,也引起了廣泛關注。相較於系統性風險(例如整體市場波動、總體經濟或利率變動帶來的影響),無法透過分散化加以消除;特質波動度(Idiosyncratic Volatility, IVOL),即個別資產本身獨有、與市場整體波動無關的風險來源,理論上可以透過多元化投資組合有效分散。
根據傳統資產定價理論,這類可分散風險不應對資產的預期報酬造成系統性影響。然而,一系列實證研究卻指出,特質波動度(IVOL) 較高的股票在未來的報酬往往顯著偏低,這一現象被稱為特質波動度之謎,並逐漸成為當代資產定價研究中的重要議題。
這項現象最早由 Ang, Hodrick, Xing, and Zhang (2006) 提出。他們以美股資料為基礎發現,即使控制 Fama-French 因子後,特質波動度(IVOL) 較高的股票依然表現較差,且該結果在後續的全球市場實證(Ang, Hodrick, Xing, and Zhang, 2009)中也得到了驗證,顯示其具有跨市場的穩健性。該研究一經發表,即引發了學界對其有效性與潛在機制的廣泛關注。
👉延伸閱讀:透過Fama&French三因子模型取得alpha,建構long-short strategy
進一步研究指出,特質波動度異象主要源自於錯誤定價與套利不對稱性(Arbitrage Asymmetry),在被高估且難以放空的標的中,IVOL 的負向關係更為明顯,因為這些股票更難以被套利(Stambaugh, Yu, and Yuan, 2014)。而這類股票通常具有小型、成長型、低獲利能力與高投資支出的特徵,因此在未來表現上顯著落後於市場平均(Detzel, Duarte, Kamara, Siegel, and Sun ,2023)。
本文後續將接續前述理論與文獻回顧,並以台灣股票市場為實證對象,重新檢視特質性波動度與未來股票報酬之間的關聯,並探討其納入投資策略的可行性。
👉延伸閱讀:什麼是「錯誤定價」? 掌握錯誤定價是否能帶來報酬?
特質波動度是否能在台灣市場重現其在美國市場所觀察到的負向異象,是一項值得深入驗證的實證課題。本節將說明樣本選取、IVOL的建構方法與分組邏輯,並透過投資組合排序法(portfolio sorting)從敘述統計、橫斷面報酬分析(Return Analysis)、資訊係數分析(Information Coefficient Analysis)、周轉率分析(Turnover Analysis)等面向,系統性評估特質波動度作為投資因子的預測能力。
本研究所使用之資料,均取自台灣經濟新報(TEJ)資料庫,並透過 TEJ API 取得下列資料表的資料:
樣本期間涵蓋 2005 年 1 月至 2025 年 3 月,研究對象為台灣上市及上櫃之普通股。
TEJ 因子資料庫中的特質波動度(IVOL)參考 Hou, Xue , and Zhang (2020) 提出的方法進行計算,計算方式如下:
為提升估計結果之穩健性,IVOL 計算時設有以下條件,滿足條件時才進行計算:
Factor Library因子資料庫 – 涵蓋動能、股息率、價值、成長等九大因子分類,高效率實踐因子投資
為進一步描述台灣市場中個股特質波動度的橫斷面分布特性,本文將每日的樣本依據 IVOL 大小由小到大排序,並將所有股票等量劃分為十個組別,以利於後續檢驗特質波動度與股票報酬之間的系統性關係。
表一呈現各組之 IVOL 敘述統計量,包括最小值、最大值、平均值、標準差以及樣本數量與比例。從結果觀察,各組 IVOL 值呈現遞增趨勢,且第 10 組的標準差明顯高於其他組別,反映高 IVOL 股票之間存在更大的異質性。
表一、特質波動度(IVOL)十分位分組之敘述統計量
本表依每日 IVOL 值排序後等量分組,各統計量是針對每一分組在整個樣本期間內所涵蓋之所有觀察值計算而得。
| 分組 | 最小值 (Min) | 最大值 (Max) | 平均值 (Mean) | 標準差 (Std) | 樣本數 (Count) | 占比 (%) |
|---|---|---|---|---|---|---|
| 1 | 0.00000 | 0.01707 | 0.00548 | 0.00212 | 746835 | 10.05 |
| 2 | 0.00424 | 0.01994 | 0.00810 | 0.00234 | 742751 | 10.00 |
| 3 | 0.00548 | 0.02233 | 0.00999 | 0.00262 | 742168 | 9.99 |
| 4 | 0.00671 | 0.02471 | 0.01183 | 0.00284 | 742329 | 9.99 |
| 5 | 0.00792 | 0.02697 | 0.01380 | 0.00300 | 742907 | 10.00 |
| 6 | 0.00934 | 0.02973 | 0.01600 | 0.00312 | 741330 | 9.98 |
| 7 | 0.01112 | 0.03211 | 0.01863 | 0.00322 | 741653 | 9.98 |
| 8 | 0.01357 | 0.03514 | 0.02199 | 0.00332 | 742271 | 9.99 |
| 9 | 0.01682 | 0.04014 | 0.02666 | 0.00361 | 741538 | 9.98 |
| 10 | 0.02173 | 1.54585 | 0.03749 | 0.00908 | 744226 | 10.02 |
為進一步了解特質波動度與公司基本特徵之間的關係,本節以月頻資料進行分析,依每月底各股票的 IVOL 值由小到大排序,並盡可能等分為十個組別。針對每一組別,計算多項基本面變數的中位數作為代表,以觀察 IVOL 水準與公司特徵之間的關係。涵蓋指標與結果摘要如表二與圖三。
以每月底 IVOL 排序,等分為十分位組別,並計算每組中所有股票各變數之中位數;Amihud 非流動性指標為過去一個月每日的報酬率絕對值與當日成交值(百萬元)的比值取平均,用以衡量每單位交易金額對於價格變動的敏感程度,當流動性較低時,價格變動幅度通常較大;借券餘額比為當日借券賣出餘額與市值的比值;融券餘額比為當日融券賣出餘額與市值的比值。
表二、特質波動度(IVOL)十分位分組與基本面特徵之關聯分析
| 指標類型 | 指標 | 結果 |
|---|---|---|
| 市值與交易資訊 | 收盤價 | IVOL 最大的組別,股價最低。 |
| 市值 | 呈現負相關(IVOL 越高,市值越小)。 | |
| Amihud 非流動性指標 | IVOL 最大的組別,非流動性明顯最高。 | |
| 估值與獲利能力 | 本益比、股價淨值比 | 呈現正相關(IVOL 越高,P/B 與 P/E 越高,估值越高)。 |
| 現金股利率 | 呈現負相關(IVOL 越高,股利越低)。 | |
| 風險面 | 總波動度 | 大致呈正相關(IVOL 越高,總波動越高)。 |
| CAPM_Beta | 大致呈正相關(IVOL 越高,與市場連動性越高)。 | |
| 法人參與度 | 外資持股率 | 作為法人持股的代理變數,在高分位數的組別呈現負相關(IVOL 越高,外資持股越低)。 |
| 籌碼面 | 借券餘額比 | 作為法人放空情緒的代理變數,低分位組呈現正相關,並且在 IVOL 最大的組別明顯最低。 |
| 融券餘額比 | 作為散戶放空情緒的代理變數,大致呈正相關(IVOL 越高,散戶放空情緒越高)。 |
另外圖三,每張子圖對應一項基本面特徵,X 軸為每月底依 IVOL 的十分位分組;每個分組的特徵值為當月組內所有個股的中位數
圖三、特質波動度(IVOL)十分位分組之各基本面特徵中位數分布
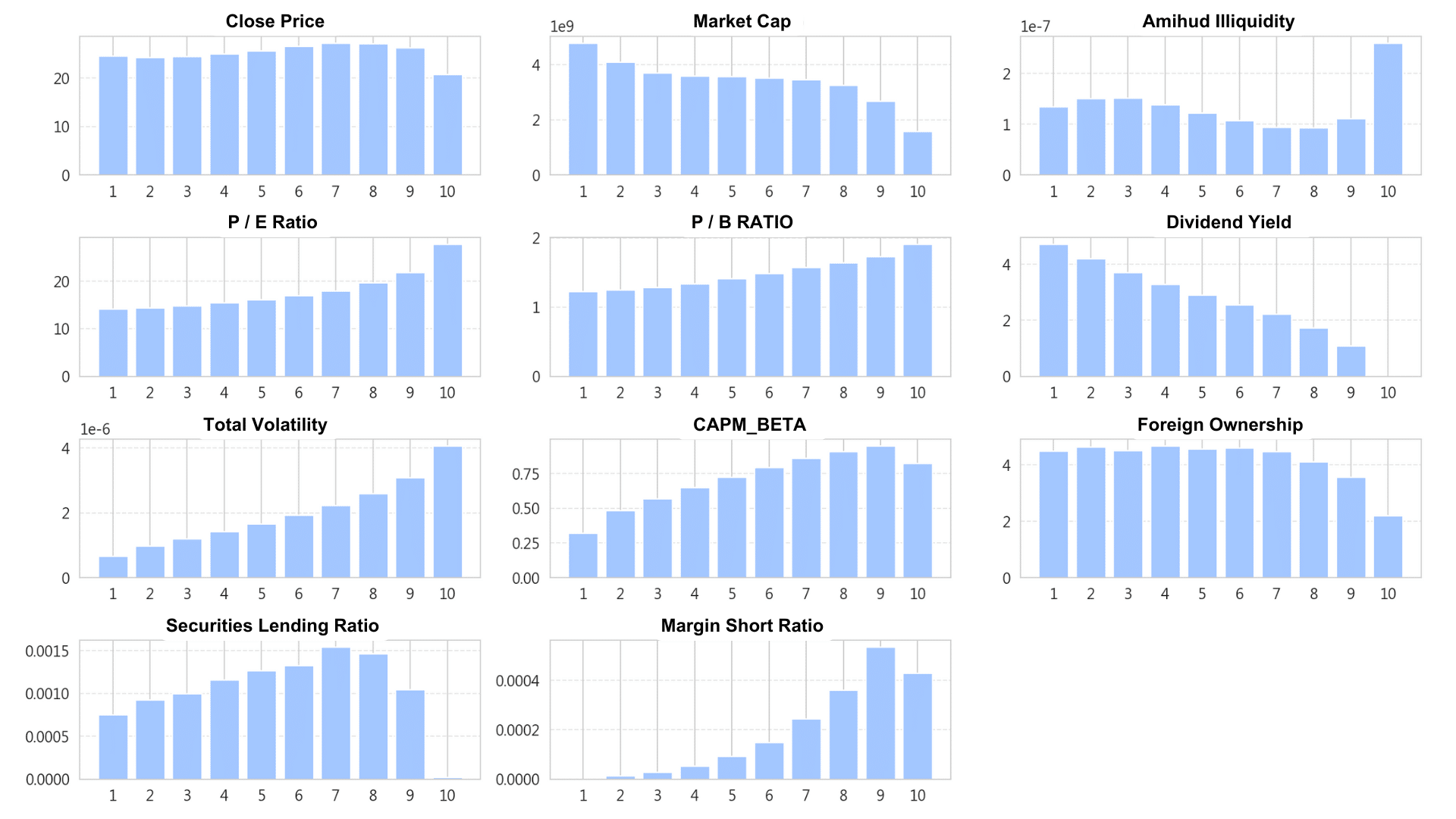
綜合上述分析,IVOL 較高的股票普遍具備市值較小、估值水準較高、外資持股比例較低、股利發放較低等特徵,整體趨近於的小型成長股。相對地,IVOL 較低的股票則多屬於市值較大、估值較低、外資持股比例較高、股利發放水準較高的公司,屬性上更接近大型價值股。這樣的結果與過去文獻(如 Novy-Marx, 2014)對高波動性股票特徵的描述基本相符,若將這類 IVOL 偏高、結構上偏向風險劣勢的標的事前篩除,或許有助於強化投資組合的整體品質與穩定性。
因子報酬分析主要是觀察不同 IVOL 分組下的平均報酬率表現,以及是否存在單調性趨勢。
觀察結果顯示,不論持有期為 1 日、5 日、10 日或 21 日,IVOL 最低組(Bottom Quantile,即第 1 組)的平均報酬率均高於 IVOL 最高組(Top Quantile,即第 10 組)。此外,多空對沖投資組合(Spread)的平均報酬率均呈現負值,顯示持有低 IVOL 股票相對持有高 IVOL 股票具有優勢。
各分組與多空對沖組的平均報酬統計結果如表三所示,本表依每日 IVOL 值排序後等量分組,並呈現 Top Quantile第 10 組、Bottom Quantile第 1 組與 Spread 多空對沖投資組合在不同持有期下的平均報酬率。
表四、IVOL 因子分組與多空對沖組合之每日平均報酬率(單位:基點(bps))
| 1日持有期 (1D) | 5日持有期 (5D) | 10日持有期(10D) | 21日持有期(21D) | |
|---|---|---|---|---|
| Top Quantile (高IVOL組) | 6.144 | 4.402 | 4.285 | 4.551 |
| Bottom Quantile (低IVOL組) | 7.330 | 6.175 | 5.790 | 5.673 |
| Spread | -1.186 | -2.435 | -2.242 | -2.012 |
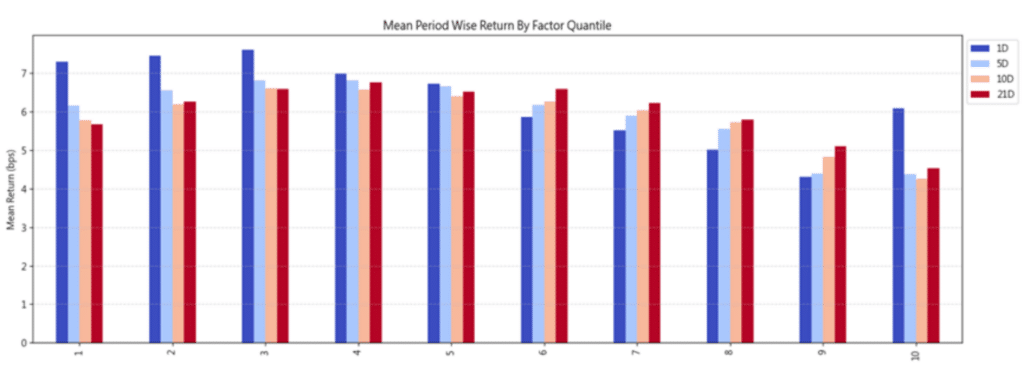
上述結果亦可由圖五直觀呈現,各持有期下的平均報酬率大致呈現隨 IVOL 升高而下降的趨勢,雖然中間組別偶有波動,但整體而言,低 IVOL 組別報酬表現普遍優於高IVOL組別。
本表依每日 IVOL 值分為十組,並計算各組未來不同持有期之平均報酬率。
圖五、IVOL因子十分位分組於不同持有期下之平均報酬率比較 (單位:基點(bps))
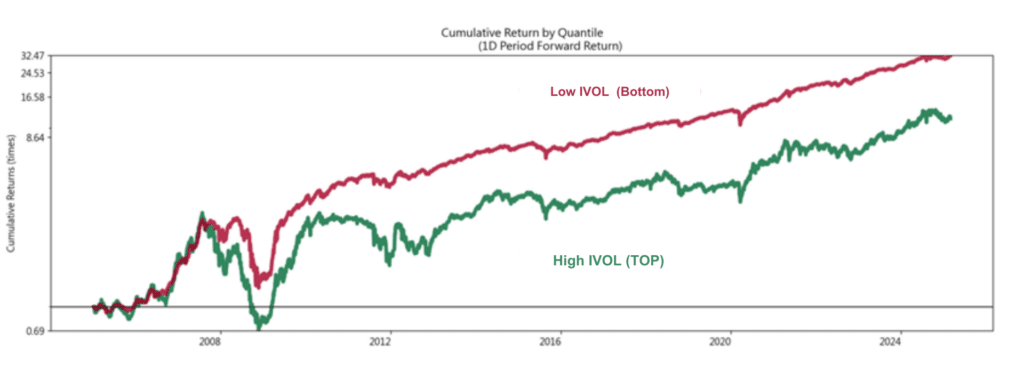
為進一步檢視 IVOL 數值大小對投資組合累積表現的影響,圖六繪製低 IVOL 組與高 IVOL 組的累積報酬率走勢圖。 圖表呈現 Top Quantile第 10 組與 Bottom Quantile 第 1 組的累積報酬率走勢;持有期為1D。
從結果觀察,低 IVOL 組別不僅在長期累積報酬上略勝一籌,更在市場波動加劇時展現出明顯較小的回撤幅度,顯示其具備較佳的防禦性特質。
圖六、IVOL 分組累積報酬率走勢圖(Top vs Bottom Quantile)
本節接著評估特質波動度的預測能力,採用斯皮爾曼等級相關係數(Spearman’s Rank Correlation Coefficient)衡量 IVOL 與未來報酬間的關聯性。資訊係數統計量整理如表七:
表七、IVOL 因子於不同持有期下之資訊係數(IC)統計摘要
| 指標 | 1日持有期(1D) | 5日持有期(5D) | 10日持有期(10D) | 21日持有期(21D) |
|---|---|---|---|---|
| IC Mean | -0.0361 | -0.0639 | -0.0754 | -0.0872 |
| IC Std | 0.1315 | 0.1267 | 0.1218 | 0.1225 |
| Risk Adjusted IC | -0.2745 | -0.504 | -0.6193 | -0.7121 |
| IC < 0(%) | 0.6073 | 0.6979 | 0.7304 | 0.7675 |
| IC < -0.03(%) | 0.5142 | 0.605 | 0.6428 | 0.6886 |
| IC < -0.05(%) | 0.4466 | 0.5388 | 0.5814 | 0.6331 |
| IC t-value | -19.3209*** | -35.478*** | -43.5908*** | -50.1253*** |
| IC p-value | 0 | 0 | 0 | 0 |
| IC Skewness | -0.0695 | 0.0055 | 0.0326 | 0.109 |
| IC Kurtosis | 0.2128 | 0.1033 | 0.156 | -0.0483 |
根據統計結果,IVOL 在各持有期間下的 IC 均值(IC Mean)皆為負值,且除 1 日持有期(1D)外,均值皆小於 -0.05,顯示其具有明顯的負向預測能力。此外,t 檢定結果均達高度顯著水準(IC p-value 皆為 0),進一步支持因子的統計可靠性。
從風險調整後IC(Risk Adjusted IC)來看,除 1D 外均小於 -0.5;而 IC 小於 0 的比例皆超過 60%,隨持有期延長至 21 日更上升至近 77%,進一步凸顯 IVOL 的預測力具有穩定性。
整體而言,特質波動度在台灣市場展現了穩定且顯著的負向預測效果。
為進一步評估特質波動度策略在實務操作上的可行性,本節衡量各分組的持股周轉率。周轉率的高低反映了換股頻率,進而影響交易成本與執行難易度。
周轉率統計量整理如表八:
表八、IVOL 因子分組於不同持有期下之平均周轉率
| 1日持有期 (1D) | 5日持有期 (5D) | 10日持有期(10D) | 21日持有期 (21D) | |
|---|---|---|---|---|
| Top Quantile (高IVOL組) | 0.088 | 0.259 | 0.389 | 0.561 |
| Bottom Quantile (低IVOL組) | 0.076 | 0.237 | 0.378 | 0.590 |
以 21 日持有期為例,Top 組與 Bottom 組投資組合的單期平均周轉率分別為 0.561 與 0.590,年化後(乘以 12)約為 6.7 至 7 倍,屬於中度周轉水準。
此結果顯示,儘管 IVOL 存在一定程度的持股更替,但整體換股頻率並不過高,交易成本與實務操作負擔仍屬可控範圍內。
本文首先建立特質波動度(IVOL)在台灣股市中的實證基礎,並揭示其對報酬表現的影響;下一篇分析文《因子研究系列|建構特質波動度的因子策略,提升投資組合的整體績效》,我們將著重於如何將此發現轉化為可操作的投資策略,從理論邁向應用,透過建構與回測單因子模型與濾波增強模型,評估如何運用 IVOL 來提升投資組合的整體績效。
透過標準化、系統化與透明的資料服務,TEJ Factor Library 因子資料庫協助使用者從資料取得、因子設計到策略落地,全流程無縫接軌,讓因子投資真正落實於日常操作之中。藉由日常更新的 Point-in-Time 架構、涵蓋九大因子類別與超過百項指標,TEJ Factor Library 因子架構已結合學術理論與台灣市場實務,提供穩健的資料基礎,協助策略回測、投資組合建構與風險管理等各環節。
面對市場不確定性與因子擴張的挑戰,唯有掌握具備可驗證性與高度彈性的資料庫,方能在因子投資浪潮中搶得先機,打造永續且具前瞻性的量化研究生態系。