Monte Carlo Simulation
Table of Contents
The purpose of Monte Carlo simulation is to estimate the likely outcome of an uncertain event, and it works by modeling the variables of the uncertain event by assuming a probability distribution. Also, each forecast period is constantly recomputing the results with a random set of numbers, resulting in a large number of possible outcomes.
In the financial field, this method is widely used to measure the return and risk of asset portfolios, focusing more on predicting extreme trends at the end. Therefore, at the end of this article, we will also illustrate the risk-return performance of the portfolio by visualizing the results.
MacOS & Jupyter Notebook
# Basic
import numpy as np
import pandas as pd# Graph
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
sns.set()# TEJ API
import tejapi
tejapi.ApiConfig.api_key = 'Your Key'
tejapi.ApiConfig.ignoretz = True
Security Transaction Data Table:Listed securities with unadjusted price and index. Code is ‘TWN/EWPRCD’.
Return Information Data Table:Listed securities with daily return. Code is ‘TWN/EWPRCD2’.
Step 1. Return Data
ticker = ['1476', '2330', '2603', '2882']
# Eclat Textile, TSMC, Cathay Financial Holdings and EVERGREENret = tejapi.get('TWN/EWPRCD2', # 公司交易資料-已調整股價(收盤價)
coid = ticker,
mdate = {'gte':'20200101'},
opts = {'columns': ['coid', 'mdate', 'roia']},
chinese_column_name = True,
paginate = True)
ret = ret.set_index('年月日')
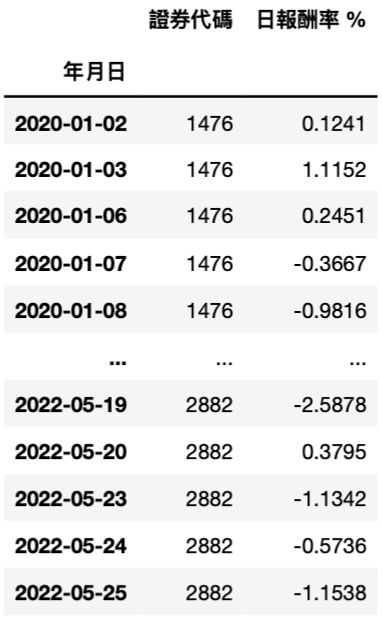
# Transpose Table
RetData = {}for i in ticker:
r = ret[ret['證券代碼'] == i]
r = r['日報酬率 %']
RetData.setdefault(i, r)RetData = pd.concat(RetData, axis = 1)
RetData = RetData * 0.01
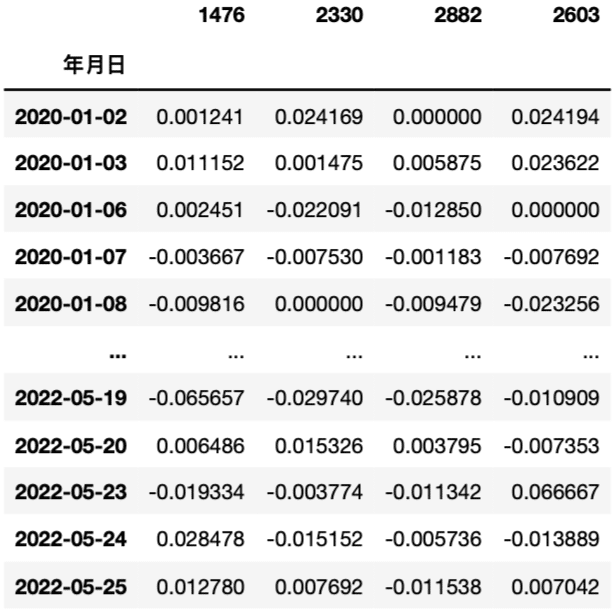
The data table format is converted here to facilitate the subsequent calculation of the average return of each target and the covariate between the targets.
Step 2. Average Return, Covariance, Principal Calculation
# Average Return
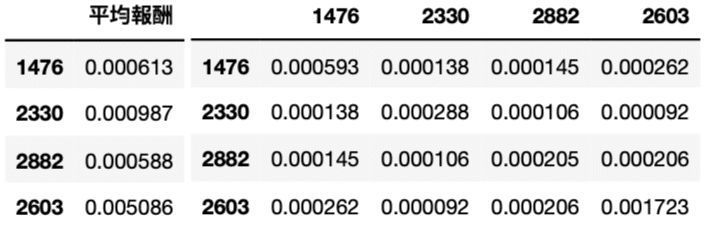
Mean = pd.DataFrame(
list(np.mean(RetData[i]) for i in RetData.columns), index=RetData.columns, columns = ['平均值'])# Covariance Matrix
covMatrix = RetData.cov()
price = tejapi.get('TWN/EWPRCD', # Unadjusted Price
coid = ticker,
mdate = {'gte':'20220525', 'lte':'20220525'},
opts = {'columns': ['coid', 'mdate', 'close_d']},
chinese_column_name = True,
paginate = True)price = price.set_index('年月日')principal = (price.loc['2020-05-25']['收盤價(元)'].sum()) * 1000
By adding up the close prices of the four underlyings on May 25, 2020, and assuming that at least one stock (1,000 shares) is held, the initial principal is $1,193,900.
Weights, Simulation Period and Number of Simulations
# Weights
weights = list()for i in range(4):
weights.append(list(price['收盤價(元)'])[i]/price['收盤價(元)'].sum())# Number
number_of_trial = 100# Period
sim_period = 30
In the part of weight setting, readers can make changes according to their own holdings of the target. We directly use the stock price weight ratio here and it is only for demonstration.
Eclat Textile:40%、TSMC:44%、EVERGREEN:12%、Cathay Financial Holdings:4%
sim_mean = np.full(shape = (sim_period, 4), fill_value = Mean.T.loc['平均報酬'])
sim_mean = sim_mean.T
First, define the storage table sim_mean and fill in the average return of each target, and then transpose it to separate the individual targets.
sim_portfolio = np.full(shape = (sim_period, number_of_trial), fill_value = 0)
Next, define the storage table sim_portfolio as the forecast field of the portfolio, and fill each field with 0 first, and then fill in the forecast value of the forecast path for the period through calculation.
for i in range(0, number_of_trial):
multi_normal = np.random.normal(size = (sim_period, 4))
cholesky = np.linalg.cholesky(covMatrix)
sim_return = sim_mean + np.inner(cholesky, multi_normal)
sim_portfolio[:,i] =
np.cumprod(np.inner(weights, sim_return.T)+1) * principal
multi_normal:
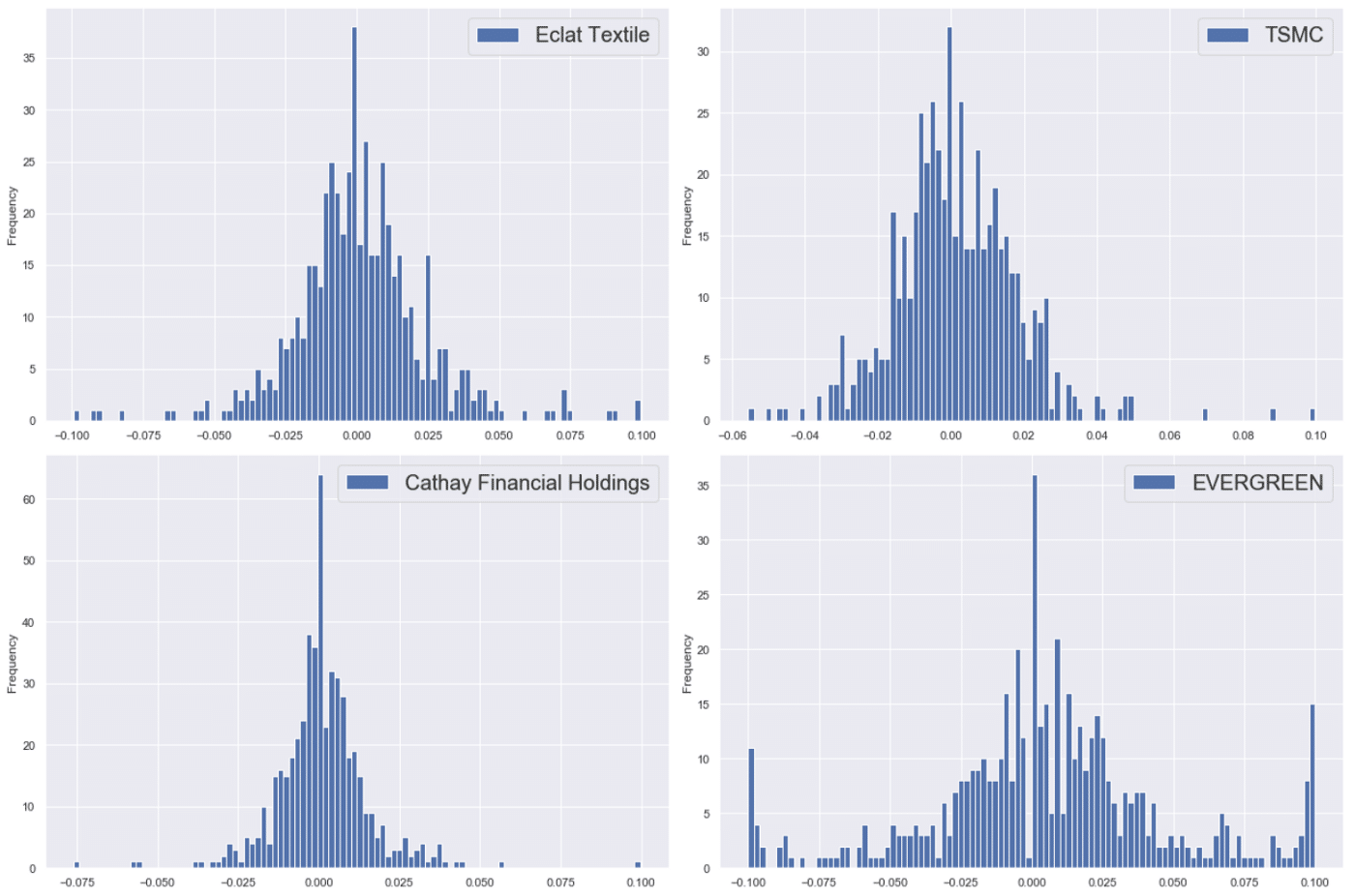
It could be seen from the above figure, except for Evergreen (2603), which has serious fat-tail problem, the distribution of return for other 3 targets are roughly close to the normal distribution, so this we apply the normal distribution to each target.
cholesky:
When dealing with multi-asset investment portfolios, the lower triangular matrix of the covariance matrix is decomposed through cholesky to deal with the correlation problem between securities.
Subsequently, take the inner product of the above two matrices to obtain the simulated return trend of each target; finally multiply the weight ratio of each target (also the inner product) and the initial principal to complete the simulation calculation of the investment portfolio path.
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS'] # Enter Chineseplt.figure(figsize=(15,8)) #Set the size of graph
plt.plot(sim_portfolio)
plt.ylabel('投資組合累積價值變動', fontsize = 15)
plt.xlabel('模擬期間', fontsize = 15)
plt.title('模擬路徑', fontsize = 20)
plt.show()
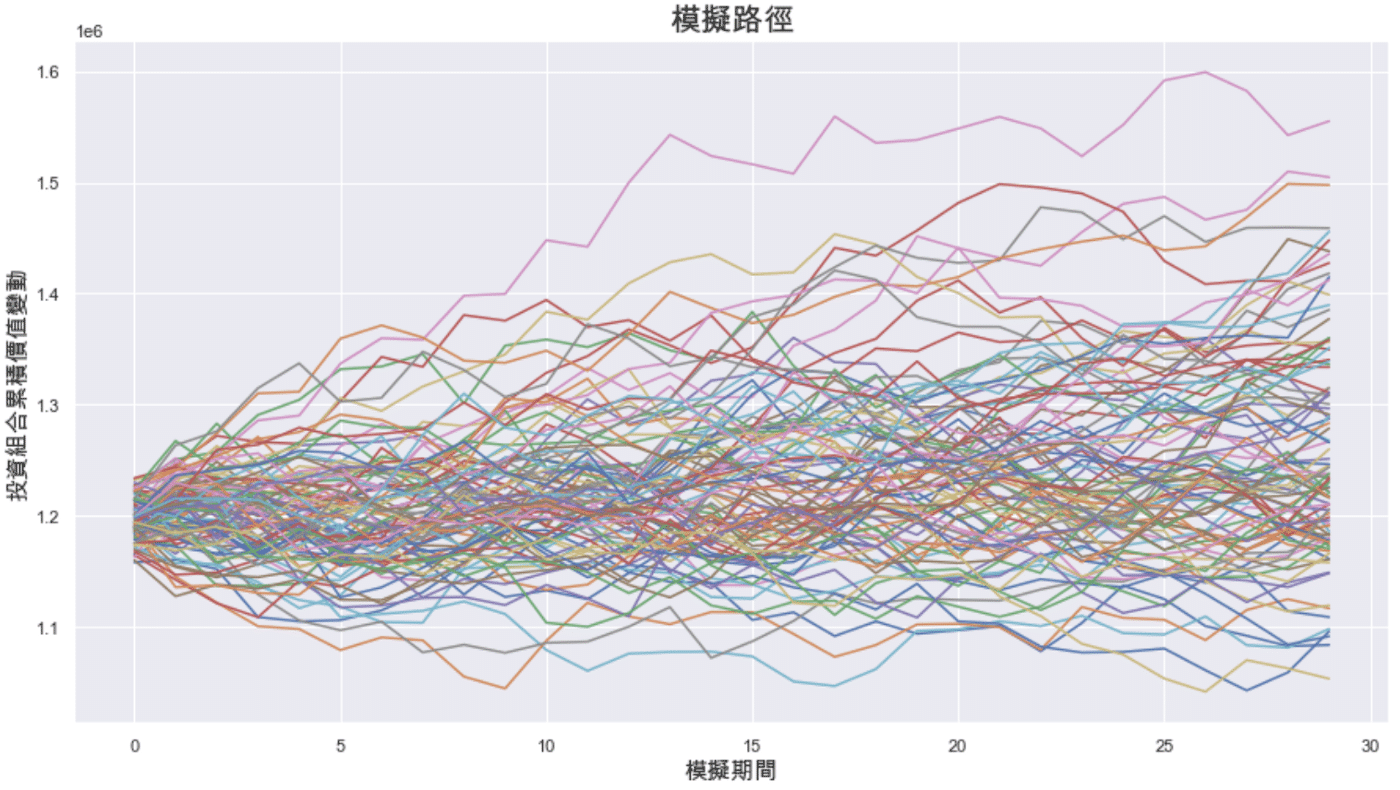
Through the simulation results this time, it can be inferred from the path at the bottom of the chart that the downside risk of the portfolio in the next month will not exceed -16% at most; while the upside return may be at most 25%. Therefore, the portfolio has lower downside risk and higher probability of upside.
Through the above process, I believe readers can understand the execution process of the Monte Carlo method and know that it is supported by statistical theory; however, because the Monte Carlo method is based on random probability The possible future trend does not mean that the market will be completely the same as the predicted result. If there is a large fluctuation in the market leading to extreme values, the reference of the Monte Carlo method will be reduced. Therefore, in order to maintain a leading position in the market, it is not only necessary to have clear and logical analysis results supported by data, but also to keep abreast of the flow of information. TEJ also welcomes readers to purchase the solutions in TEJ E Shop, I believe that readers have complete After the database, you can easily complete the trend simulation of your own asset allocation, and grasp the overall pulse of the market.