
This guide will introduce the types of data analysis used in quantitative research, then discuss relevant examples and applications in the finance industry.
Table of Contents
Quantitative data analysis is the process of interpreting meaning and extracting insights from numerical data, which involves mathematical calculations and statistical reviews to uncover patterns, trends, and relationships between variables.
Beyond academic and statistical research, this approach is particularly useful in the finance industry. Financial data, such as stock prices, interest rates, and economic indicators, can all be quantified with statistics and metrics to offer crucial insights for informed investment decisions. To illustrate this, here are some examples of what quantitative data is usually used for:
Ultimately, quantitative data analysis helps investors navigate the complex financial landscape and pursue profitable opportunities.

Although quantitative data analysis is a powerful tool, it cannot be used to provide context for your research, so this is where qualitative analysis comes in. Qualitative analysis is another common research method that focuses on collecting and analyzing non-numerical data, like text, images, or audio recordings to gain a deeper understanding of experiences, opinions, and motivations. Here’s a table summarizing its key differences between quantitative data analysis:
| Research Method | Quantitative Analysis | Qualitative Analysis |
| Types of Data Used | Numerical data: numbers, percentages, etc. | Non-numerical data: text, images, audio, narratives, etc |
| Perspective | More objective and less prone to bias | More subjective as it may be influenced by the researcher’s interpretation |
| Data Collection | Closed-ended questions, surveys, polls | Open-ended questions, interviews, observations |
| Data Analysis | Statistical methods, numbers, graphs, charts | Categorization, thematic analysis, verbal communication |
| Focus | What and how much | Why and how |
| Best Use Case | Measuring trends, comparing groups, testing hypotheses | Understanding user experience, exploring consumer motivations, uncovering new ideas |
Due to their characteristics, quantitative analysis allows you to measure and compare large datasets; while qualitative analysis helps you understand the context behind the data. In some cases, researchers might even use both methods together for a more comprehensive understanding, but we’ll mainly focus on quantitative analysis for this article.
Once you have your data collected, you have to use descriptive statistics or inferential statistics analysis to draw summaries and conclusions from your raw numbers.
As its name suggests, the purpose of descriptive statistics is to describe your sample. It provides the groundwork for understanding your data by focusing on the details and characteristics of the specific group you’ve collected data from.
On the other hand, inferential statistics act as bridges that connect your sample data to the broader population you’re truly interested in, helping you to draw conclusions in your research. Moreover, choosing the right inferential technique for your specific data and research questions is dependent on the initial insights from descriptive statistics, so both of these methods usually go hand-in-hand.
With sophisticated descriptive statistics, you can detect potential errors in your data by highlighting inconsistencies and outliers that might otherwise go unnoticed. Additionally, the characteristics revealed by descriptive statistics will help determine which inferential techniques are suitable for further analysis.
One of the key statistical tests used for descriptive statistics is central tendency. It consists of mean, median, and mode, telling you where most of your data points cluster:
Another statistic to test in descriptive analysis is the measures of dispersion, which involves range and standard deviation, revealing how spread out your data is relative to the central tendency measures:
The shape of the distribution will then be measured through skewness.
While the core measures mentioned above are fundamental, there are additional descriptive statistics used in specific contexts, including percentiles and interquartile range.
Let’s illustrate these concepts with a real-world example. Imagine a financial advisor analyzing a client’s portfolio. They have data on the client’s various holdings, including stock prices over the past year. With descriptive statistics they can obtain the following information:
By calculating these descriptive statistics, the advisor gains a quick understanding of the client’s portfolio performance and risk distribution. For instance, they could use correlation analysis to see if certain stock prices tend to move together, helping them identify expansion opportunities within the portfolio.
While descriptive statistics provide a foundational understanding, they should be followed by inferential analysis to uncover deeper insights that are crucial for making investment decisions.
Inferential statistics analysis is particularly useful for hypothesis testing, as you can formulate predictions about group differences or potential relationships between variables, then use statistical tests to see if your sample data supports those hypotheses.
However, the power of inferential statistics hinges on one crucial factor: sample representativeness. If your sample doesn’t accurately reflect the population, your predictions won’t be very reliable.
Here are some of the commonly used tests for inferential statistics in commerce and finance, which can also be integrated to most analysis software:
If you’re a financial analyst studying the historical performance of a particular stock, here are some predictions you can make with inferential statistics:
Understanding these inferential analysis techniques can help you uncover potential relationships and group differences that might not be readily apparent from descriptive statistics alone. Nonetheless, it’s important to remember that each technique has its own set of assumptions and limitations. Some methods are designed for parametric data with a normal distribution, while others are suitable for non-parametric data.
Now that we have discussed the types of data analysis techniques used in quantitative research, here’s a quick guide to help you choose the right method and grasp the essential steps of quantitative data analysis.
Choosing between all these quantitative analysis methods may seem like a complicated task, but if you consider the 2 following factors, you can definitely choose the right technique:
The data used in quantitative analysis can be categorized into two types, discrete data and continuous data, based on how they’re measured. They can also be further differentiated by their measurement scale. The four main types of measurement scales include: nominal, ordinal, interval or ratio. Understanding the distinctions between them is essential for choosing the appropriate statistical methods to interpret the results of your quantitative data analysis accurately.
Discrete data, which is also known as attribute data, represents whole numbers that can be easily counted and separated into distinct categories. It is often visualized using bar charts or pie charts, making it easy to see the frequency of each value. In the financial world, examples of discrete quantitative data include:
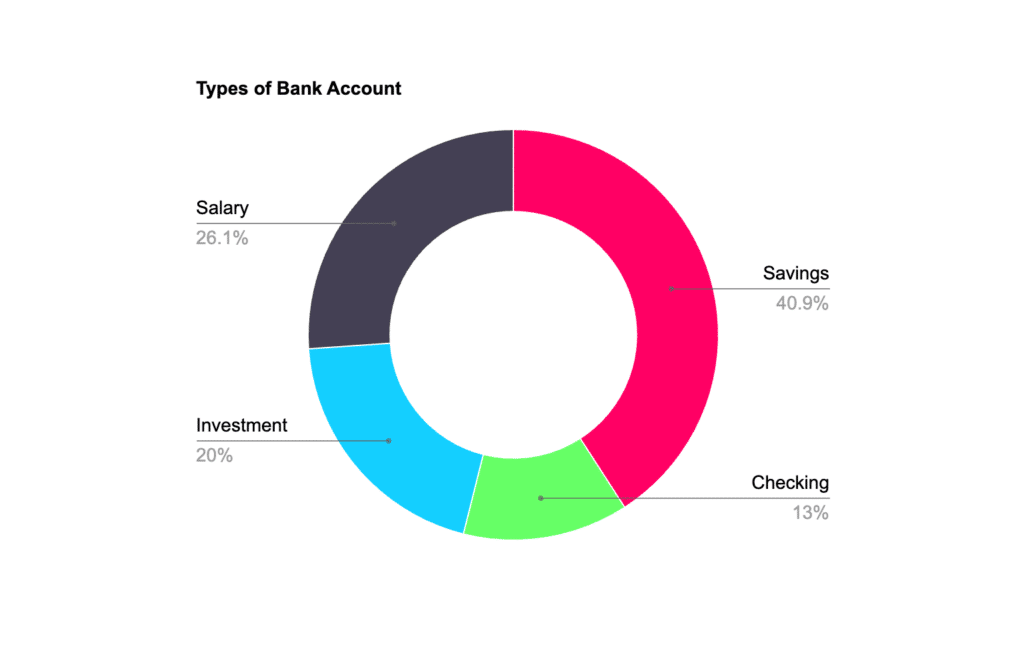
Discrete data usually use nominal or ordinal measurement scales, which can be then quantified to calculate their mode or median. Here are some examples:
Conversely, continuous data can take on any value and fluctuate over time. It is usually visualized using line graphs, effectively showcasing how the values can change within a specific time frame. Examples of continuous data in the financial industry include:
Source: Freepik
The measurement scale for continuous data is usually interval or ratio. Here is breakdown of their differences:
You also need to make sure that the analysis method aligns with your specific research questions. If you merely want to focus on understanding the characteristics of your data set, descriptive statistics might be all you need; if you need to analyze the connection between variables, then you have to include inferential statistics as well.
Depending on your research question, you might choose to conduct surveys or interviews. Distributing online or paper surveys can reach a broad audience, while interviews allow for deeper exploration of specific topics. You can also choose to source existing datasets from government agencies or industry reports.
Raw data might contain errors, inconsistencies, or missing values, so data cleaning has to be done meticulously to ensure accuracy and consistency. This might involve removing duplicates, correcting typos, and handling missing information.
Furthermore, you should also identify the nature of your variables and assign them appropriate measurement scales, it could be nominal, ordinal, interval or ratio. This is important because it determines the types of descriptive statistics and analysis methods you can employ later. Once you categorize your data based on these measurement scales, you can arrange the data of each category in a proper order and organize it in a format that is convenient for you.
Based on the measurement scales of your variables, calculate relevant descriptive statistics to summarize your data. This might include measures of central tendency (mean, median, mode) and dispersion (range, standard deviation, variance). With these statistics, you can identify the pattern within your raw data.
Then, these patterns can be analyzed further with inferential methods to test out the hypotheses you have developed. You may choose any of the statistical tests mentioned above, as long as they are compatible with the characteristics of your data.
Now that you have the results from your statistical analysis, you may draw conclusions based on the findings and incorporate them into your business strategies. Additionally, you should also transform your findings into clear and shareable information to facilitate discussion among stakeholders. Visualization techniques like tables, charts, or graphs can make complex data more digestible so that you can communicate your findings efficiently.
We’ve compiled some commonly used quantitative data analysis tools and software. Choosing the right one depends on your experience level, project needs, and budget. Here’s a brief comparison:
| Tools | Learning Curve | Suitable For | Licensing |
| Microsoft Excel | Easiest | Beginners & basic analysis | One-time purchase with Microsoft Office Suite |
| SPSS | Easy | Social scientists & researchers | Paid commercial license |
| Minitab | Easy | Students & researchers | Paid commercial license or student discounts |
| SAS | Moderate | Businesses & advanced research | Paid commercial license |
| Stata | Moderate | Researchers & statisticians | Paid commercial license |
| Python | Moderate (Coding optional) | Programmers & data scientists | Free & Open-Source |
| R | Steep (Coding required) | Experienced users & programmers | Free & Open-Source |
| Mathematica | Steep (Coding required) | Scientists & engineers | Paid commercial license |
| Matlab | Steep (Coding required) | Scientists & engineers | Paid commercial license |
So how does this all affect the finance industry? Quantitative finance (or quant finance) has become a growing trend, with the quant fund market valued at $16,008.69 billion in 2023. This value is expected to increase at the compound annual growth rate of 10.09% and reach $31,365.94 billion by 2031, signifying its expanding role in the industry.
Quant finance is the process of using massive financial data and mathematical models to identify market behavior, financial trends, movements, and economic indicators, so that they can predict future trends.These calculated probabilities can be leveraged to find potential investment opportunities and maximize returns while minimizing risks.
There are several common quantitative strategies, each offering unique approaches to help stakeholders navigate the market:
This strategy aims for high returns with low volatility. It employs sophisticated algorithms to identify minuscule price discrepancies across the market, then capitalize on them at lightning speed, often generating short-term profits. However, its reliance on market efficiency makes it vulnerable to sudden market shifts, posing a risk of disrupting the calculations.
This strategy identifies and invests in assets based on factors like value, momentum, or quality. By analyzing these factors in quantitative databases, investors can construct portfolios designed to outperform the broader market. Overall, this method offers diversification and potentially higher returns than passive investing, but its success relies on the historical validity of these factors, which can evolve over time.
This approach prioritizes portfolio balance above all else. Instead of allocating assets based on their market value, risk parity distributes them based on their risk contribution to achieve a desired level of overall portfolio risk, regardless of individual asset volatility. Although it is efficient in managing risks while potentially offering positive returns, it is important to note that this strategy’s complex calculations can be sensitive to unexpected market events.
Quant analysts are beginning to incorporate these cutting-edge technologies into their strategies. Machine learning algorithms can act as data sifters, identifying complex patterns within massive datasets; whereas AI goes a step further, leveraging these insights to make investment decisions, essentially mimicking human-like decision-making with added adaptability. Despite the hefty development and implementation costs, its superior risk-adjusted returns and uncovering hidden patterns make this strategy a valuable asset.
Quantitative data analysis relies on objective, numerical data. This minimizes bias and human error, allowing stakeholders to make investment decisions without emotional intuitions that can cloud judgment. In turn, this offers reliable and consistent results for investment strategies.
Quantitative analysis generates precise numerical results through statistical methods. This allows accurate comparisons between investment options and even predictions of future market behavior, helping investors make informed decisions about where to allocate their capital while managing potential risks.
By analyzing large datasets and identifying patterns, stakeholders can generalize the findings from quantitative analysis into broader populations, applying them to a wider range of investments for better portfolio construction and risk management
Quantitative research is more suited to analyze large datasets efficiently, letting companies save valuable time and resources. The softwares used for quantitative analysis can automate the process of sifting through extensive financial data, facilitating quicker decision-making in the fast-paced financial environment.
By focusing on numerical data, quantitative analysis may provide a limited scope, as it can’t capture qualitative context such as emotions, motivations, or cultural factors. Although quantitative analysis provides a strong starting point, neglecting qualitative factors can lead to incomplete insights in the financial industry, impacting areas like customer relationship management and targeted marketing strategies.
Breaking down complex phenomena into numerical data could cause analysts to overlook the richness of the data, leading to the issue of oversimplification. Stakeholders who fail to understand the complexity of economic factors or market trends could face flawed investment decisions and missed opportunities.
In conclusion, quantitative data analysis offers a deeper insight into market trends and patterns, empowering you to make well-informed financial decisions. However, collecting comprehensive data and analyzing them can be a complex task that may divert resources from core investment activity.
As a reliable provider, TEJ understands these concerns. Our TEJ Quantitative Investment Database offers high-quality financial and economic data for rigorous quantitative analysis. This data captures the true market conditions at specific points in time, enabling accurate backtesting of investment strategies.
Furthermore, TEJ offers diverse data sets that go beyond basic stock prices, encompassing various financial metrics, company risk attributes, and even broker trading information, all designed to empower your analysis and strategy development. Save resources and unlock the full potential of quantitative finance with TEJ’s data solutions today!
Read More:
➤ Understanding Alternative Data & Its Role in Finance
➤ What is ESG Data & How Does It Empower Financial Decisions?

Subscribe to newsletter