
Table of Contents
在投資領域中,「景氣循環」向來是一個重要的參考依據。無論是總體經濟的波動、企業獲利的起伏,還是市場投資氣氛的演變,都在不同的景氣階段呈現出鮮明的差異。因此,若能掌握景氣循環的動向,便可協助投資人更精準地調整資產配置,並在投資市場中取得相對優勢。
在臺灣,政府透過「景氣燈號」的發布,提供了簡潔易懂的經濟狀態指標。景氣燈號分為藍燈、黃藍燈、綠燈、黃紅燈、紅燈五種,每一種燈號都代表了當前經濟的景氣程度:
此一燈號系統由國發會根據多項經濟指標計算得出,將複雜的總體經濟資訊轉化為一般大眾易於理解的形式。若能適時地運用這些指標,並結合量化投資策略加以驗證,投資人便可在經濟循環的波動中,掌握更適切的進出場時機。
從景氣週期角度而言,市場每隔幾年就會經歷一次熊市,造成短期間資產的顯著縮水。而我們期望景氣信號燈的資訊中可以獲取相對有力地進出場機會,使得即便是投資大盤或是 0050 這種市值型ETF,也可以通過「擇時」的方式避開下跌危機,減少投組風險。
本文章的交易邏輯為在景氣信號燈出現「藍燈」的時候進場買股票,表示當時可能會是相對低基期。並且在「紅燈」時出場賣出股票,表示當時可能是景氣過熱期。通過這樣簡單的設計,我們期望可以「避開在熊市持有部位」,並且獲取「投資大盤」的主要漲幅。同時在離開股市時,投資一年期的美債ETF,減少因持有現金而被通膨吃掉的風險。
交易標的 & 實際操作細節:
交易標的為 0050 ETF ,因為一般投資人想要投資大盤最直接的方式就是投資市值型 ETF。而債券部位選擇 00865B 美國短期公債ETF基金,選擇美國債券是因為美債相比於台灣公債殖利率來得更高,選擇短債則是希望保本的同時獲取利息收入即可,我們的目的是在離開股市時可以對抗通膨即可。
實際操作細節:由於 TEJAPI 有提供台灣景氣信號燈的分數,因此本文使用 TEJ 的景氣信號燈作為回測時的依據。
import tejapi
import pandas as pd
import numpy as np
tejapi.ApiConfig.api_key = "your key"
tejapi.ApiConfig.api_base = "your base"
# ========================================================
# 下載景氣信號燈的分數資料
data = tejapi.get('GLOBAL/ANMAR', mdate={'gte':'2000-01-01', 'lte':'2025-04-09'}, coid = 'EA1101')
# ========================================================
# 下載 0050 ETF 以及 00865B ETF 的調整後價格資料
data2 = tejapi.get('TWN/AAPRCDA', coid = ['0050'], mdate={'gte':'2000-01-01', 'lte':'2025-04-09'})
df_price = data2[['mdate','close_d', 'avgclsd']].copy()
data3 = tejapi.get('TWN/AAPRCDA', coid = ['00865B'], mdate={'gte':'2000-01-01', 'lte':'2025-04-09'})
df_bond = data3[['mdate','close_d', 'avgclsd']].copy()
# ========================================================
data['mdate'] = pd.to_datetime(data['mdate'])
data['val_shifted'] = data['val'].shift(1)
df_price['mdate'] = pd.to_datetime(df_price['mdate'])
df_bond['mdate'] = pd.to_datetime(df_bond['mdate'])data = data.set_index('mdate', drop=False)
df_price = df_price.set_index('mdate', drop=False)
df_bond = df_bond.set_index('mdate', drop=False)
df_P_daily = data.resample('D').ffill()df = df_price.join(df_P_daily, how = 'left', rsuffix='_P')
df = df.join(df_bond, how = 'left', rsuffix='_bond')
df['mdate'] = df['mdate'].dt.strftime('%Y-%m-%d')
df['mdate'] = pd.to_datetime(df['mdate'])
# ========================================================
# 將兩筆資料視覺化,觀察其過去情況
import matplotlib.pyplot as plt
fig, axes = plt.subplots(nrows=3, ncols=1, figsize=(20, 10), sharex=True)
plt.style.use('ggplot')
axes[1].plot(df['mdate'], df['avgclsd'], label = '0050 Price')
axes[1].set_title(f'0050 History Price')
axes[1].legend()
axes[0].plot(df['mdate'], df['val_shifted'], label = 'SCORE')
axes[0].axhline(y = 38, label = 'Red Light Bound', color = 'red', linestyle = '--')
axes[0].axhline(y= 16, label = 'Blue Light Bound', color = 'blue', linestyle = '--')
axes[0].set_title(f'SCORE')
axes[0].legend()
axes[2].plot(df['mdate'], df['avgclsd_bond'], label = 'Short_term_bond Price')
axes[2].set_title(f'00865B Short_term_bond History Price')
axes[2].legend()
plt.tight_layout()
plt.show()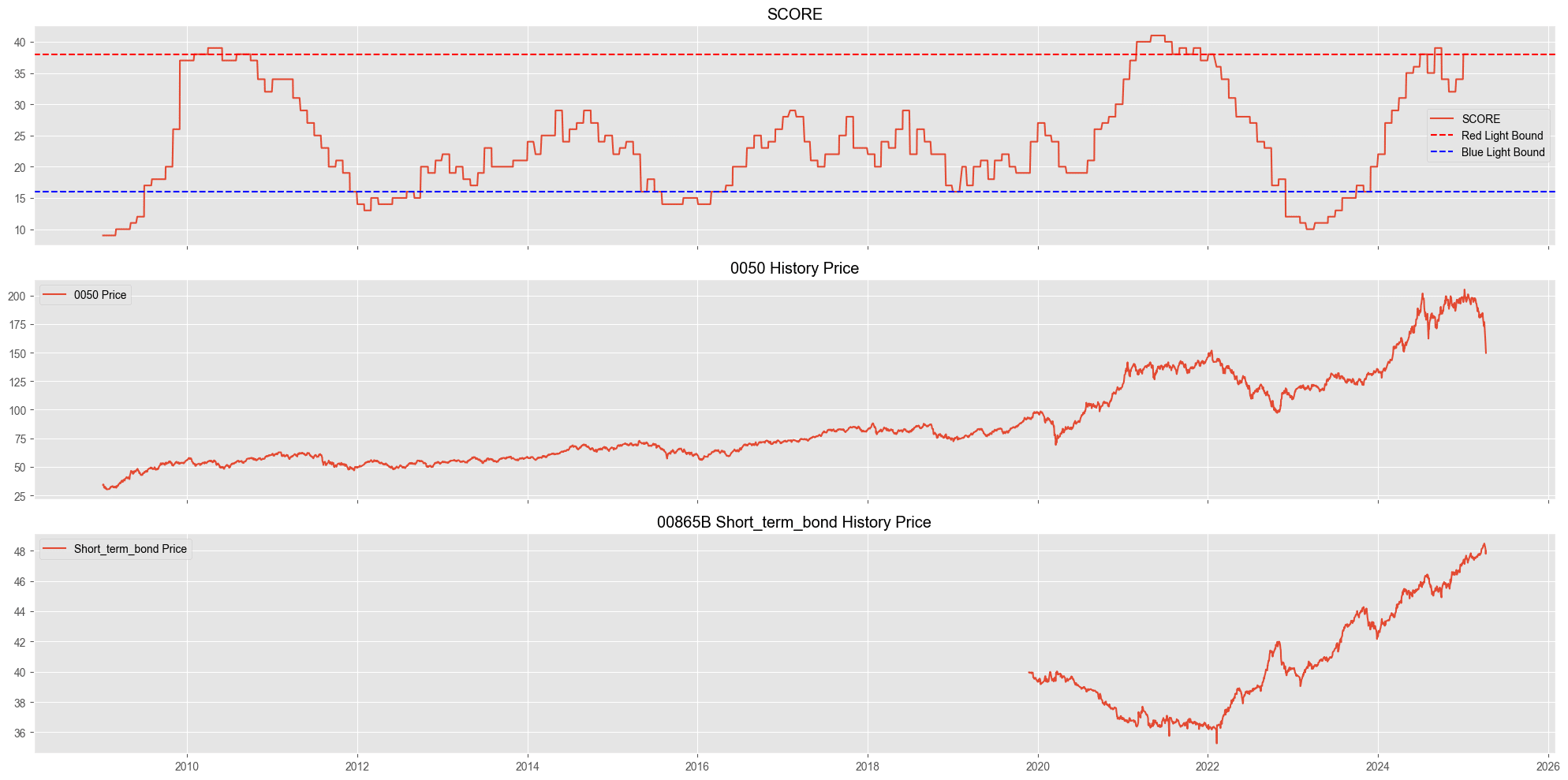
# ========================================================
# 匯入回測所需的資料
import os
import tejapi
plt.rcParams['font.family'] = 'Arial'
tej_key = "your key"
os.environ['TEJAPI_BASE'] = "your base"
os.environ['TEJAPI_KEY'] = tej_key
from zipline.data.run_ingest import simple_ingest
from zipline.api import set_slippage, set_commission, set_benchmark, symbol, record
from zipline.api import order_target_percent, order_percent, order
from zipline.api import set_long_only, set_max_leverage
from zipline.finance import commission, slippage
from zipline import run_algorithm
pool = ['0050', 'IR0001', '00865B', '00687B']
start_date = '2009-01-01'
end_date = '2025-04-09'
start_ingest = start_date.replace('-', '')
end_ingest = end_date.replace('-', '')
simple_ingest(name = 'tquant' , tickers = pool , start_date = start_ingest , end_date = end_ingest)
# ========================================================
# 以下為回測邏輯的程式碼範例
def initialize(context, pool = pool):
set_slippage(slippage.TW_Slippage(spread = 0.3 , volume_limit = 1))
set_commission(commission.Custom_TW_Commission(min_trade_cost=20, discount=1.0, tax = 0.003))
set_benchmark(symbol('IR0001'))
context.i = 0
context.pool = pool
context.state = False
context.score = None
context.hedge_state = None
context.buy_date = []
context.sell_date = []
context.a = 0
context.b = 0
context.bond = symbol('00865B')
context.stock = symbol('0050')
def handle_data(context, data, score_data = df):
backtest_date = data.current_dt.date()
today_data = score_data[score_data['mdate'].shift(1) == pd.to_datetime(backtest_date)]
context.score = today_data['val_shifted'].iloc[-1]
record(score=context.score)
if context.score <= 16 and context.state == False:
order_target_percent(context.stock, 1.0)
print(f"Date: {backtest_date}, Score: {context.score}, 買進 0050")
context.buy_date.append(pd.to_datetime(backtest_date))
context.state = True
if context.hedge_state == True:
order_target_percent(context.bond, 0)
print(f"Date: {backtest_date}, Score: {context.score},賣出債券")
context.hedge_state = False
if context.score >= 38 and context.state == True:
order_target_percent(context.stock, 0)
print(f"Date: {backtest_date}, Score: {context.score}, 賣出 0050")
context.sell_date.append(pd.to_datetime(backtest_date))
context.state = False
if context.hedge_state == False :
order_target_percent(context.bond, 1.0)
print(f"Date: {backtest_date}, Score: {context.score},買入債券避險")
context.hedge_state = True
if context.score > 16 and context.score < 38 and context.a == 0:
context.a = 1
print('進入景氣循環')
if context.state == False:
order_target_percent(context.stock, 1.0)
print(f"Date: {backtest_date}, Score: {context.score}, 買進 0050")
context.buy_date.append(pd.to_datetime(backtest_date))
context.state = True
# 因為 00685B 從 2019-11-25 才開始被交易
if pd.to_datetime(backtest_date) >= pd.to_datetime('2019-11-25') and context.b == 0:
context.b = 1
context.hedge_state = False
def analyze(context, perf):
plt.style.use('ggplot')
fig, axes = plt.subplots(nrows=2, ncols=1, figsize=(18, 10), sharex=True)
axes[0].plot(perf.index, perf['algorithm_period_return'], label = 'strategy')
axes[0].plot(perf.index, perf['benchmark_period_return'], label = 'benchmark')
for idx, i in enumerate(context.buy_date):
if idx == 0:
axes[0].axvline(x = i, color = 'red', label = 'buy 0050 & sell bond', linestyle = '--', alpha = 0.5)
axes[0].axvline(x = i, color = 'red', linestyle = '--', alpha = 0.5)
for idx, i in enumerate(context.sell_date):
if idx == 0:
axes[0].axvline(x = i, color = 'black', label = 'sell 0050 & buy bond', linestyle = '--', alpha = 0.5)
axes[0].axvline(x = i, color = 'black', linestyle = '--', alpha = 0.5)
axes[0].set_title(f'Algorithm_period_return')
axes[0].legend()
axes[1].bar(perf.index, perf['score'], label='score')
axes[1].set_title('Business cycle index')
axes[1].legend()
plt.show()
results = run_algorithm(
start = pd.Timestamp('2020-01-01', tz = 'utc'),
end = pd.Timestamp('2025-04-08', tz = 'utc'),
initialize = initialize,
handle_data = handle_data,
analyze = analyze,
bundle = 'tquant',
capital_base = 1e5)# ==================== 回測輸出結果 =====================
進入景氣循環
Date: 2020-01-02, Score: 27.0, 買進 0050
Date: 2021-02-26, Score: 40.0, 賣出 0050
Date: 2021-02-26, Score: 40.0,買入債券避險
Date: 2022-11-30, Score: 12.0, 買進 0050
Date: 2022-11-30, Score: 12.0,賣出債券
Date: 2024-06-28, Score: 38.0, 賣出 0050
Date: 2024-06-28, Score: 38.0,買入債券避險
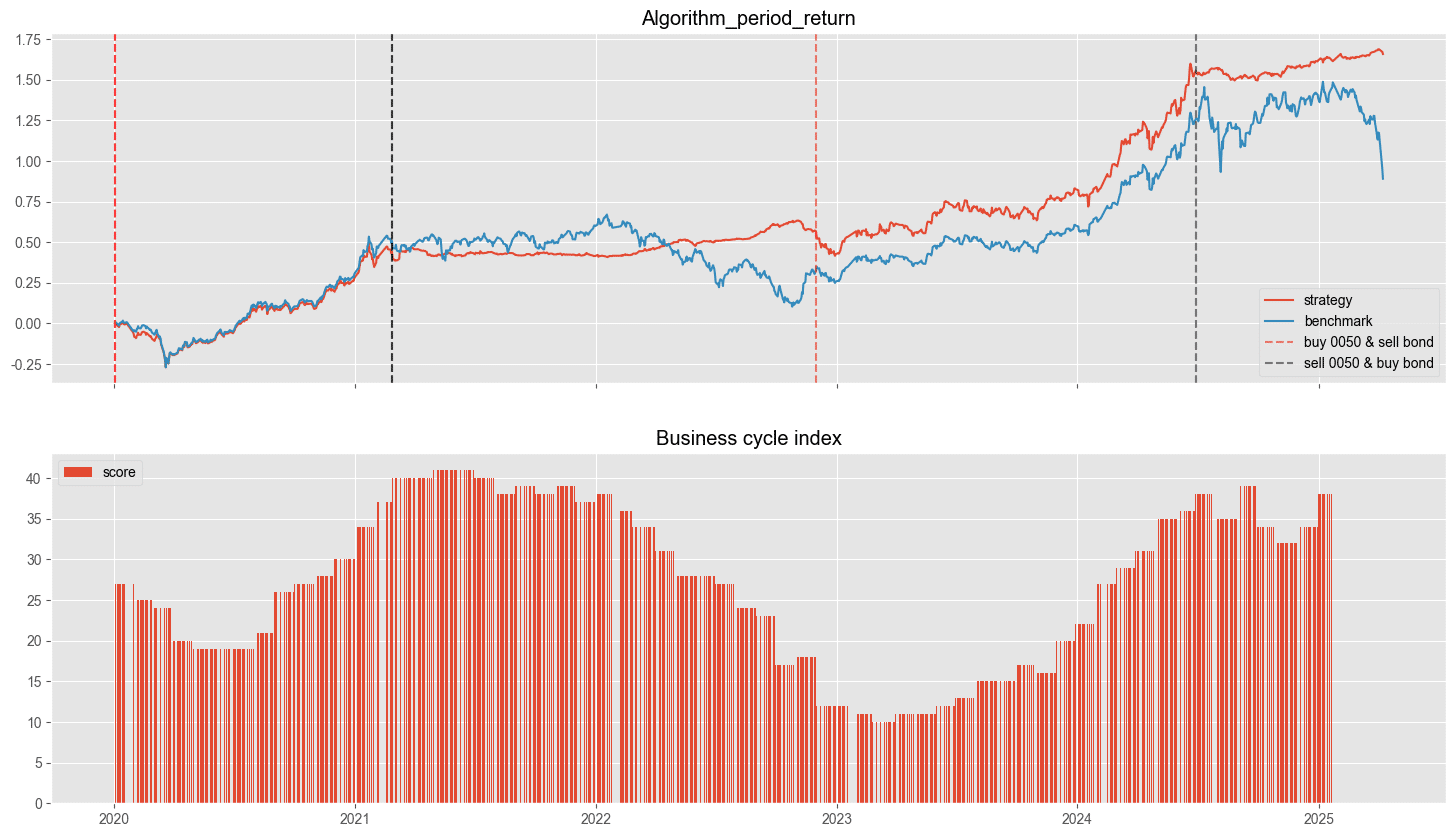
上圖為策略回測的累積報酬率圖表,圖中有標示哪個時期持有 0050 哪個時期持有短天期美債。從整體績效來看,策略整體報酬率贏過大盤非常多的,即便不算上 2025-04 出的美國關稅政策造成的股價下跌,策略依舊贏過大盤 25% 左右的報酬率。再從細部去查看,首先 2021 年至 2022 年末,大盤是先盤整一年後進入下跌段,綜合起來這兩年大盤整體報酬略為下跌,同時這段期間策略是持有美國短天期國債 ETF ,雖然漲幅不大但能夠穩定拿到利息收入的同時避開了股市下跌的波動度,這也是當初我們期望策略效果。接下來看到 2024/06 的時期,策略是賣出 0050 並且買入短債,並且在持有債券期間大盤經歷了兩次的重大下跌,第一次為 2024/08 的日圓平倉套利事件以及 2025/04 的川普關稅政策。雖然這是從後設角度去看事情,但我們可以了解當時的整體市場估值本來就推得蠻高的,即便沒有這些政策出現股市創高的動力也有限。
此策略只使用了景氣信號燈的資訊,投資人可以自行在交易邏輯上加入自己偏好的景氣指標來創建屬於自己的景氣週期策略,像是 VIX 、基準利率或採購經理人指數等等,來強化策略回測的「擇時能力」並且獲取長期穩定的報酬。
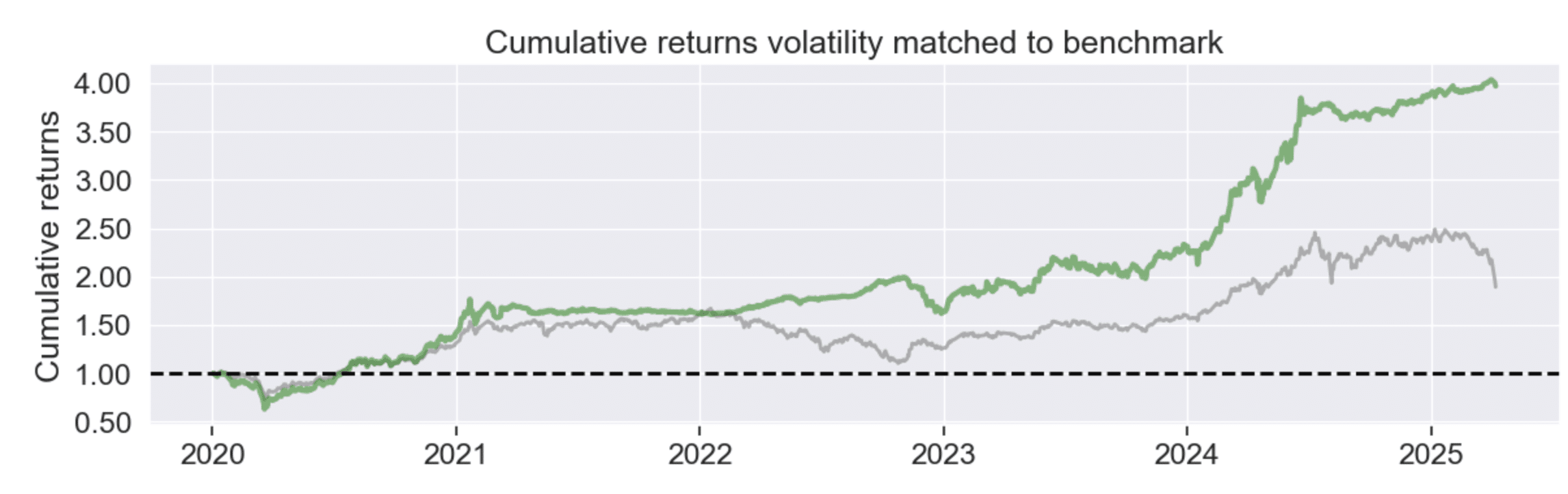
回測期間為2020-01-01至2025-04-08,選擇從 2020 開始是因為 00865B 這檔 ETF是從2019年末才上市可被交易。策略的夏普值為1.38,表示出策略很好的在控制風險下獲取不錯的報酬。
第二張圖是權衡了風險的累積報酬圖,可以看出策略在回測時確實出現了波動度較小的情況,造成整體報酬差距擴大,表示確實避開了熊市的波動時期,減少了熊市來臨時投資人的焦慮情緒。
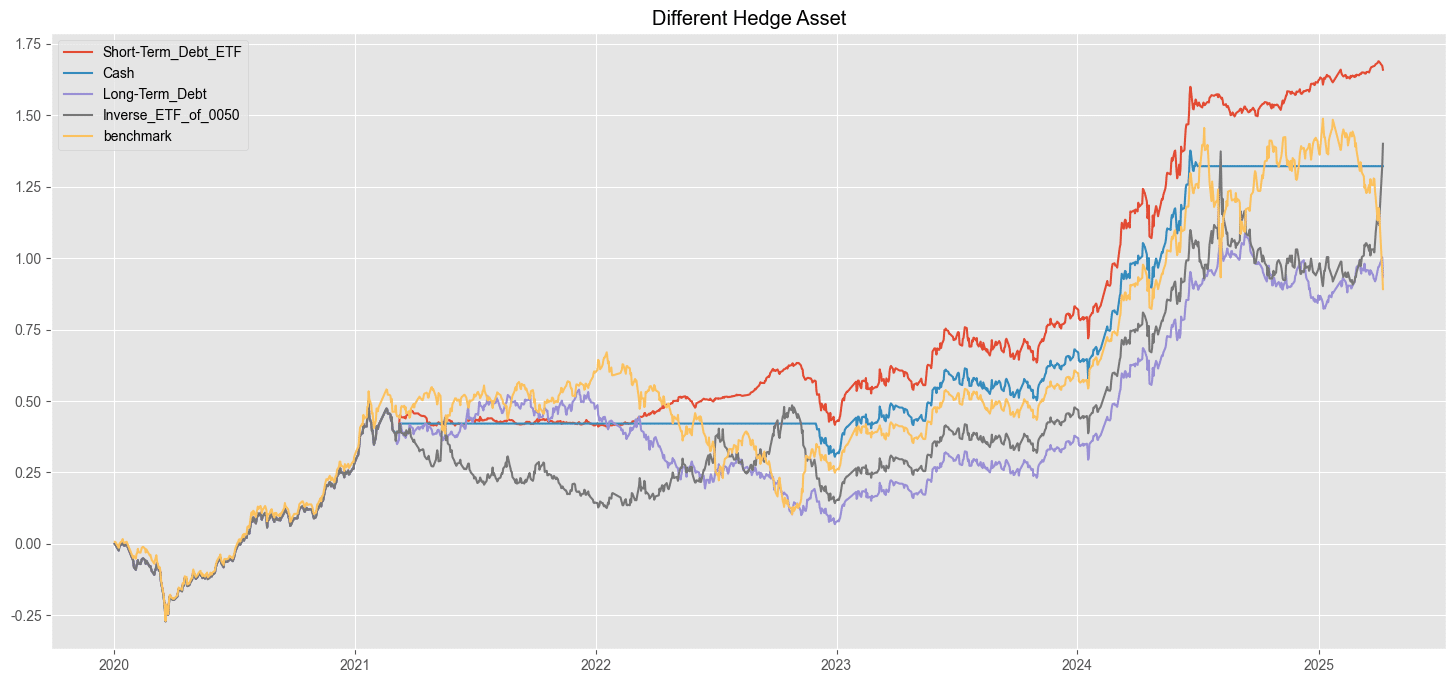
接下來呈現的圖為考慮不同的避險資產的策略比較,原始的策略(紅色線)使用的是短天期美債ETF,現在納入持有現金(藍色線)、長天期美債 ETF00687B(紫色線)以及 0050 反向型 ETF 00664R(灰色線)的情況,基準線(黃色線)為單純持有 0050 的情況。
圖中顯示績效最好的依舊是短天期美債,其次為 0050 反向型 ETF,再來是現金,最差為長天期美債。但這並不是說長天期美債的避險效果弱於短天期和現金,是因為長天期美債的價格除了利率以外還被市場的投資人預期(將習或升息預期)心態所影響。因此要以長天期美債作為避險資產,會需要研究分析更多的數據和指標。
績效第二好的為 0050 反向型 ETF ,但讀者可以發現該策略是因為 2025-04 的關稅政策造成短期間大漲,從波動來看明顯是四個策略中最大的,而且反向型 ETF 的內部資產結構可能會有期貨等衍生性金融商品,因此長期持有會造成因換倉成本而侵蝕掉原有的獲利,需要讀者額外注意!
| 避險資產 | Short Term Debt ETF | Long term Debt ETF | Cash | Inverse ETF of 0050 | Benchmark |
| 年化報酬率 | 21.3% | 13.9% | 18.11% | 18.89% | 12.37% |
| 累積報酬率 | 165.9% | 93.5% | 132.2% | 140% | 80.4% |
| 波動度 | 14.8% | 17.7% | 14.3% | 20.9% | 20.12% |
| 夏普值 | 1.38 | 0.83 | 1.23 | 0.93 | 0.68 |
| Alpha | 0.16 | 0.09 | 0.12 | 0.23 | 0 |
| Beta | 0.4 | 0.38 | 0.43 | – 0.07 | 0.92 |
從夏普值來看,表現最佳的依舊是短天期美債 ETF 達到了1.38,年化報酬率為21.3%,這對於「擇時」的策略來說是很好的表現。次好的是現金(夏普值 = 1.23),再來是反向型 ETF (夏普值 = 0.93),最後是長天期美債 ETF(夏普值 = 0.83)。對於投資人來說需要注意的是希望在市場過熱期承受多少風險,來決定投資哪種避險資產。
歡迎投資朋友參考,之後也會持續介紹使用 TEJ 資料庫來建構各式指標,並回測指標績效,所以歡迎對各種交易回測有興趣的讀者,選購 TQuant Lab 的相關方案,用高品質的資料庫,建構出適合自己的交易策略。
溫馨提醒,本次分析僅供參考,不代表任何商品或投資上的建議。
機器學習算法 XGBoost 提升技術指標一目均衡表的投資績效