事件型因子研究：透過填息機率選股

前言

我們在先前的文章《認識除權息 & 填權息》，簡單介紹過填權息的概念。填息意味著公司股票在除息日之後的價格，高於除息日前一天的收盤價格，代表買入該股票的投資者在收到股利後，還能避免股價調整後的資本損失。因此，許多投資者都著眼於買進高殖利率同時也能填息的股票，期許在收穫穩定的現金股利同時，還能夠安全出場免於資本損失。

因此本研究使用事件研究法，檢驗過往填息機率越高的股票，是否表未來填息的機率也越高，以此做為投資人在買賣高股息股票時的參考。

• 編輯環境與模組需求

本文使用Windows 11系統和Jupyter Notebook作為編輯器。

• 資料導入與環境設定

套件引入與環境參數設定

import tejapi 
import os 
import warnings 
warnings.filterwarnings('ignore')
 
os.environ['TEJAPI_KEY'] = 'Your Api Key' 
import numpy as np 
import pandas as pd 
import matplotlib.pyplot as plt 
plt.style.use('ggplot') 

plt.rcParams['font.family'] = ['DejaVu Sans', 'Arial', 'Microsoft JhengHei'] 
plt.rcParams['axes.unicode_minus'] = False  

樣本資料：2013/01/01至2025/05/01，所有曾上市櫃並且發放股利之普通股(含KY股)。

• get_universe：抓取2013/01/01至2025/05/01所有曾上市櫃的普通股股票代碼。
• simple_ingest：綁入指定期間與股票池的相關價量和基本面資料。
• tejapi：抓取tej資料庫中的填權息資料（TWN/AREINT）表，作為本次研究的樣本事件來源。
• get_bundle、get_fundamentals：將前面simple_ingest綁入的資料匯出成dataframe，方便後續研究進行整併分析。

from zipline.sources.TEJ_Api_Data import get_universe 
from zipline.data.run_ingest import simple_ingest 
from zipline.master import get_calendar 

pool = get_universe('20130101', '20250501', mkt = ['TWSE', 'OTC'], stktp_e = ['Common Stock', 'Common Stock-Foreign']) 
simple_ingest(name = 'tquant' , tickers = pool + ['IR0001'], start_date = '20130101' , end_date = '20250501') 

simple_ingest(name = 'fundamentals' , tickers =  pool + ['IR0001'], start_date = '20130101' , end_date = '20250501' , fields = ['Market_Cap_Dollars', 'r403']) 

from zipline.data.data_portal import get_bundle_price, get_fundamentals 

bundle_price = get_bundle_price(pd.Timestamp('20130101', tz='utc'), pd.Timestamp('20250501', tz='utc')) 

bundle_price['date'] = bundle_price['date'].dt.tz_convert(None) 

fundamentals = get_fundamentals(start_dt=pd.Timestamp('20130101', tz='utc'), end_dt=pd.Timestamp('20250501', tz='utc')) 

fundamentals['date'] = pd.to_datetime(fundamentals['date']) 

df = tejapi.fastget('TWN/AREINT', coid = pool, mdate={'gte': '20130101', 'lte': '20250501'}, paginate = True, chinese_column_name = True) 

date = get_calendar('TEJ').sessions_in_range('20130101', '20250501').tz_convert(None) 

close = bundle_price.pivot(index='date', columns='symbol', values='close')

指標計算

本研究欲探討公司過往填權息的機率與未來股票報酬間是否存在相關性，因此使用填權息資料表中的填權息（Y/N）進行後續計算。

• 計算填權息機率（cover_prob），每家公司累加填權息（Y/N）欄位為Y的樣本數除以各家總樣本數。
• 使用上一期的填權息機率取lag一期為近期填權息機率（last_cover_prob），作為每期分類股票之依據。

from zipline.master import get_calendar 

date = get_calendar('TEJ').all_sessions.tz_convert(None) 

dividend = df[['證券碼', '除權息日', '填權息(Y/N)']].rename({'證券碼': 'symbol'}, axis=1) 

dividend['last_date'] = dividend['除權息日'].apply(lambda x: date[date.searchsorted(x)-1]) 

dividend['cover_prob'] = dividend.groupby('symbol')['填權息(Y/N)'].transform(lambda x: x.eq('Y').cumsum() / np.arange(1, len(x)+1)) 

dividend['last_cover_prob'] = dividend.groupby('symbol')['cover_prob'].transform(lambda x: x.shift(1))

排除無近期填息機率的樣本後，總筆數為13640筆，如下圖所示。

圖一、樣本公司填權息機率

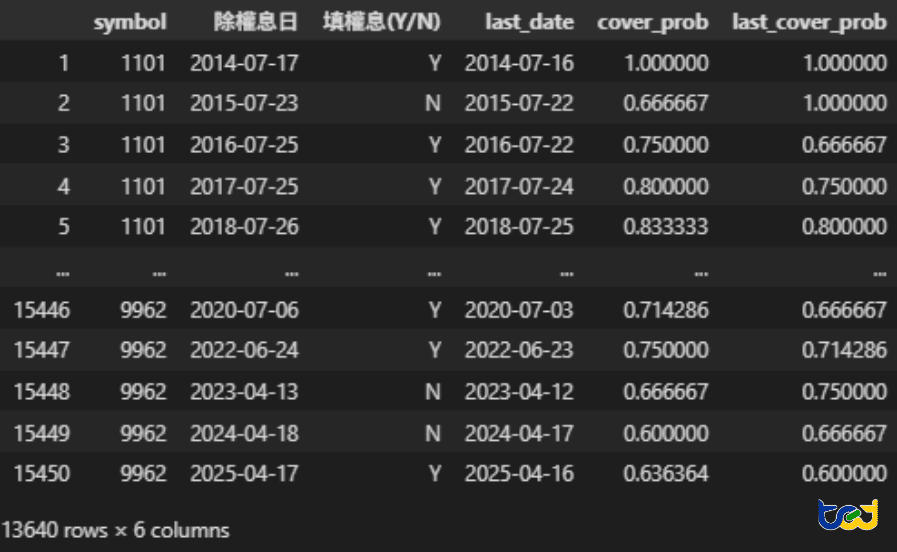
資料來源：TEJ 填權息資料庫

利用事件研究法，了解填息機率對股價報酬的影響

事件研究法常用來分析公司發生特定事件前後，市場對該公司股票的反應是否存在顯著的異常報酬（Abnormal Return, AR），以及在該事件前後的累積異常報酬（Cumulative Abnormal Return, CAR）是否能持續顯著，若此事件存有顯著的異常報酬與累積異常報酬，則可預期未來當公司再次發生相同事件時，投資者可進場買入該公司股票賺取顯著正報酬。

• TEJ事件研究系統->四步驟完成分析研究，點我了解詳情

而在事件研究法中最關鍵點莫過於預期報酬的估計方式，常見估計方式有平均調整模式、市場指數調整模式、OLS估計法與GARCH估計法等眾多方法，本研究使用市場指數調整模式，主要分析公司在經歷特定事件後的股票報酬是否能超過同期市場指數報酬，從而出現顯著異常報酬值。

• ret：使用前面經simple_ingest綁入的調整後收盤價計算個股報酬率。
• benchmark：使用get_Benchmark_Return函式載入2013/01/01至2025/05/01期間的加權報酬指數日報酬。

from zipline.sources.TEJ_Api_Data import get_Benchmark_Return 

ret = bundle_price.pivot(index='date', columns='symbol', values='close_adj').pct_change().fillna(0) 

benchmark = get_Benchmark_Return('20130101', '20250501', 'IR0001') 

benchmark.index = benchmark.index.tz_localize(None) 

excess_ret = ret.apply(lambda x: x - benchmark).round(5)

本研究欲分析投資者是否能依據過往的填息機率來做為選股依據，在賺到股利同時也能順利填息避免資本損失，因此使用最後買進日作為事件日（T），並且取前後21個交易日作為事件窗口，觀察公司在最後買進日前後約一個月期間的異常報酬變化。

• bef_ret：取每檔股票於T-21至T-1日期間的異常報酬。
• aft_ret：取每檔股票於T至T+21日期間的異常報酬。
• 填息機率分組：由於原本之填息機率為0~100%之間數值，較難以觀察機率值與事件日前後異常報酬關係，因此將原本數值分為五組，即0~20%、20~40%、40~60%、60~80%、80~100%等五組。

dividend['aft_ret'] = dividend.apply(lambda x: excess_ret.loc[x['last_date']:, x['symbol']].head(22).tolist(), axis=1) 

dividend['bef_ret'] = dividend.apply(lambda x: excess_ret.loc[:x['last_date'], x['symbol']].tail(22).head(21).tolist(), axis=1) 

sample = dividend[['last_cover_prob', 'bef_ret', 'aft_ret']] 

bef_ret = sample['bef_ret'].apply(lambda x: pd.Series(x, index=[f"T-{i}" for i in range(21, 0, -1)])) 

aft_ret = sample['aft_ret'].apply(lambda x: pd.Series(x, index=[f"T{i}" for i in range(len(x))])) 
 
sample1 = sample[['last_cover_prob']].join(bef_ret.join(aft_ret)).reset_index(drop=1).set_index("last_cover_prob") 

sample1.index = pd.cut(sample1.index, bins=np.arange(0, 1.2, 0.2), labels=[f"{i}-{i+20}" for i in np.arange(0, 100, 20)]) 

import plotly.graph_objects as go 
from plotly.subplots import make_subplots 

car = sample1.groupby(level=0).mean().cumsum(axis=1).mul(100) 

ar = sample1.groupby(level=0).mean().mul(100) 

fig = go.Figure() 

 fig = make_subplots(rows=5, cols=1, row_heights=[60] * 5,  
                    subplot_titles=[f"填息機率：{i}%" for i in ar.index], vertical_spacing=0.08) 

for row, index in enumerate(ar.index): 

    fig.add_trace(go.Bar(x=ar.columns, y=ar.loc[index], name='平均異常報酬', marker_color='blue', opacity=0.6, showlegend=(row == 0)),  row=row+1, col=1, ) 

    fig.add_trace(go.Scatter(x=car.columns, y=car.loc[index], mode='lines+markers', name='累積平均異常報酬', line=dict(color='red'),  showlegend=(row == 0),), row=row+1, col=1, ) 

    fig.update_xaxes(ticktext=ar.columns, tickvals=ar.columns) 

    fig.update_yaxes(title='異常報酬(%)', row=row+1, col=1) 

fig.update_layout( 
    height=1500, 
    title="最後交易日前後21天異常報酬與累積異常報酬－各填息機率區間", 
    legend_title=" ", 
    showlegend=True, 
    legend=dict( 
        yanchor="top", 
        y=1.08, 
        xanchor="right", 
        x=1 
    ) 
) 

fig.add_vline(x=21, line_width=3, line_dash="dash", annotation_text='最後交易日') 

fig.show()

結果分析

使用plotly.express進行視覺化以後，從下圖可以看出填息機率在40~100%之間的組別，累積平均異常報酬走勢均十分相近，從表格的期間AAR(%)累積值也能看出，在T-21~T-11這兩週中，股價均沒有顯著異於同期大盤的變化。但等到T-10~T-3這一週期間，三組的股價均顯著增長，帶動各自組別的CAAR(%)成長至0.433%~0.513%且達1%顯著水平，顯示出過往高填息機率的股票，投資人傾向在最後買進日前兩週左右期間進場布局，但也有可能是因為除息公告日大多距離除息日前兩週公布，投資人接收到後才陸續進場買入，不過可以確定的是，多數投資人會提前一週時間至過往填息機率高的股票中布局，從而在最後買進日前墊高了股價。

T-2~T2期間除去80~100%的組別，40~60%與60~80%兩組股價相對平穩，並沒有顯著為正的CAAR(%)，推測是由於此前已進場的投資人趕在T-2~T-1日期間將股票賣出，趁多數散戶欲進場賺股利時出場，反而使該兩日連續出現負的AAR(%)，導致就算後續T與T1兩日出現正的AAR(%)，整段T-2~T2期間也沒有達到顯著為正的CAAR(%)。等到最後T3~T21期間，三組均呈現一致的賣壓走勢，CAAR(%)分別達到-0.840%、-0.583%、-0.446%且均達1%顯著水平，推測是投資人在收穫股利且股票順利填息後旋即賣出，導致股價在除息後基本一路呈現負的異常報酬。

▶️延伸閱讀：事件型因子研究：公司宣告發放股利

圖二、最後交易日前後21天異常報酬與累積異常報酬 – 各填息機率區間

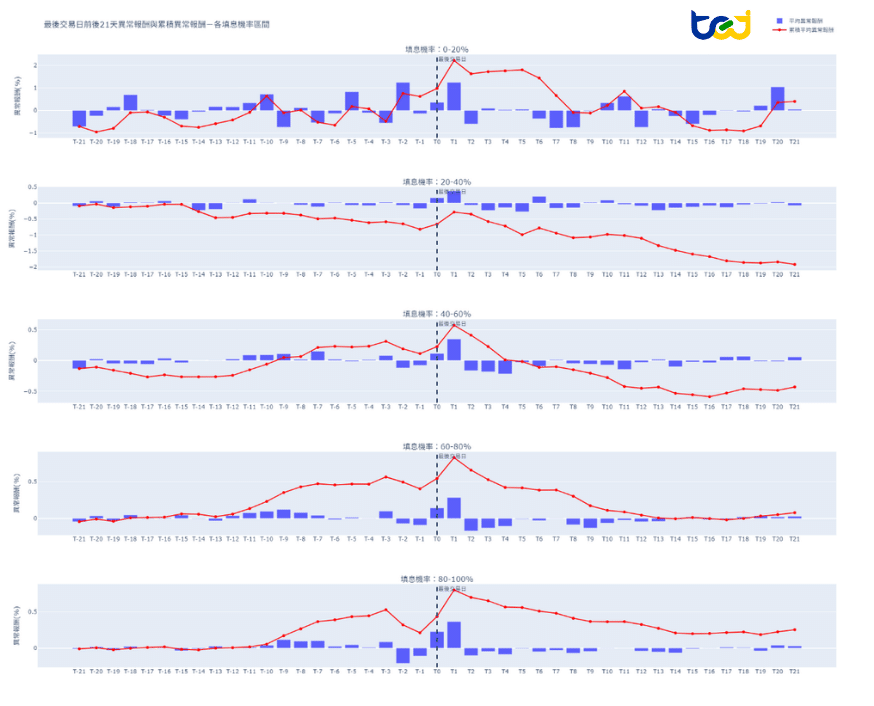
資料來源：TEJ資料庫整理

圖三、各填息機率區間樣本公司最後交易日前後AAR(%)

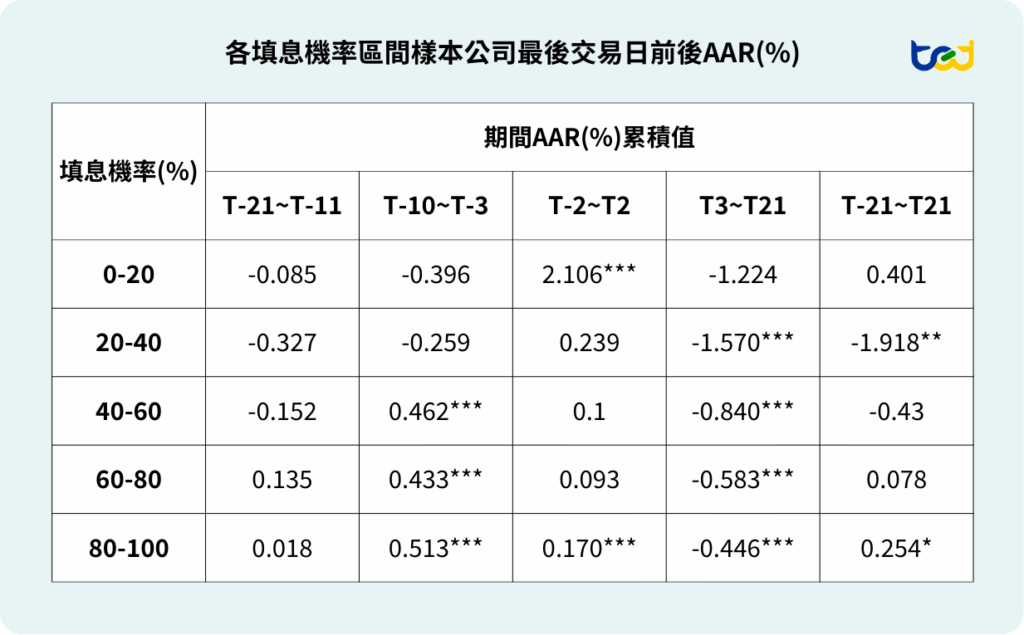
註：*代表單樣本t檢定達10%內顯著水平；**代表5%內顯著水平；***代表1%內顯著水平。

資料來源：TEJ資料庫整理

納入營運指標分析

本研究進一步納入營業利益成長率進行分析，營業利益率為評估公司在本業獲利表現的重要指標之一，當一間公司的營業利益成長率為正，代表其本業上的獲利能力正逐步成長，而股價長期以來多為反映公司營運表現，因此多增加該指標可望進一步從高填息股票中找出未來更有可能填息之股票。

dividend1 = dividend.merge(bundle_fundamentals, left_on=['last_date', 'symbol'], right_on=['date', 'symbol'], how='left') 

dividend1['growth_bin'] = pd.cut(dividend1['Operating_Income_Growth_Rate_Q'], [-np.inf, 0, np.inf], labels=['decrease', 'increase']) 

dividend1['cover_bin'] = pd.cut(dividend1['last_cover_prob'], np.arange(0, 1.2, 0.2), labels=[f"{i}-{i+20}" for i in np.arange(0, 100, 20)])  

bef_ret = dividend1.dropna(subset=['cover_bin', 'growth_bin']).reset_index().set_index(['index', 'cover_bin', 'growth_bin'])['bef_ret'].apply(lambda x: pd.Series(x, index=[f"T-{i}" for i in range(21, 0, -1)])) 

aft_ret = dividend1.dropna(subset=['cover_bin', 'growth_bin']).reset_index().set_index(['index', 'cover_bin', 'growth_bin'])['aft_ret'].apply(lambda x: pd.Series(x, index=[f"T{i}" for i in range(len(x))]))  

sample2 = bef_ret.join(aft_ret) 

import plotly.graph_objects as go 
from plotly.subplots import make_subplots 

car = sample2.groupby(level=[1, 2]).mean().cumsum(axis=1).mul(100) 

ar = sample2.groupby(level=[1, 2]).mean().mul(100) 

fig = go.Figure() 

fig = make_subplots(rows=5, cols=1, row_heights=[60] * 5,  
                    subplot_titles=[f"填息機率：{i}%" for i in ar.index.get_level_values(0).unique()], vertical_spacing=0.08) 

for row, index in enumerate(ar.index.get_level_values(0).unique()): 

    fig.add_trace(go.Scatter(x=ar.columns, y=ar.loc[index].loc['increase'].cumsum(), mode='lines+markers', name='累積平均異常報酬（利益率正成長）', line=dict(color='red'), showlegend=(row == 0),), row=row+1, col=1, )  

    fig.add_trace(go.Scatter(x=ar.columns, y=ar.loc[index].loc['decrease'].cumsum(), mode='lines+markers', name='累積平均異常報酬（利益率負成長）', line=dict(color='blue'), showlegend=(row == 0),), row=row+1, col=1, ) 

    fig.update_xaxes(ticktext=ar.columns, tickvals=ar.columns) 

    fig.update_yaxes(title='異常報酬(%)', row=row+1, col=1) 

fig.update_layout( 
    height=1500, 
    title="最後交易日前後21天異常報酬與累積異常報酬－各填息機率區間", 
    legend_title=" ", 
    showlegend=True, 
    legend=dict( 
        yanchor="top", 
        y=1.08, 
        xanchor="right", 
        x=1 
    ) 
) 

fig.add_vline(x=21, line_width=3, line_dash="dash", annotation_text='最後交易日') 

fig.add_hline(y=0, line_width=1, line_dash="solid") 

fig.show()

從下圖各填息區間的紅藍線可以看出，除了0~20%區間的組別外，其餘組別的CAAR(%)在經由營業利益成長率區分後，均有更為顯著的正負向走勢。同樣對於40~100%之間的三組來分析，原先在T-21~T-11這兩週中，CAAR(%)均處於不顯著的走勢，與大盤差異不大，但經過進一步區分後，可以看出投資人針對過往填息機率高且本業上有所成長之公司會更早的進場布局。

反之，當本業上表現不佳有所衰退，就算是過往填息機率高的股票，投資人也並不會買單。

進一步到T-10~T-3這一週區間後，CAAR(%)表現又更為提升，光這期間就達到0.730%~0.816%且均達1%顯著水平，顯示市場投資人的加速進場布局，不斷拉高股票的異常報酬。而在後續的T3~T21期間，雖然60~100%等兩組別同樣出現部分下滑，但相比於前面未經過成長率區分時顯著為負的CAAR(%)來說，走勢明顯更為緩降，並無顯著的賣壓出現導致落後大盤。而對於負向成長率的組別來說則更為明顯，三組的CAAR(%)分別達到1%顯著的-1.194%、-0.907%與-0.785%，突顯出投資人並不相信公司在除息後的表現，從而使得股價在除息後也只是加速下跌，加大與同期大盤走勢的差異。

圖四、最後交易日前後21天異常報酬與累積異常報酬 – 各填息機率區間

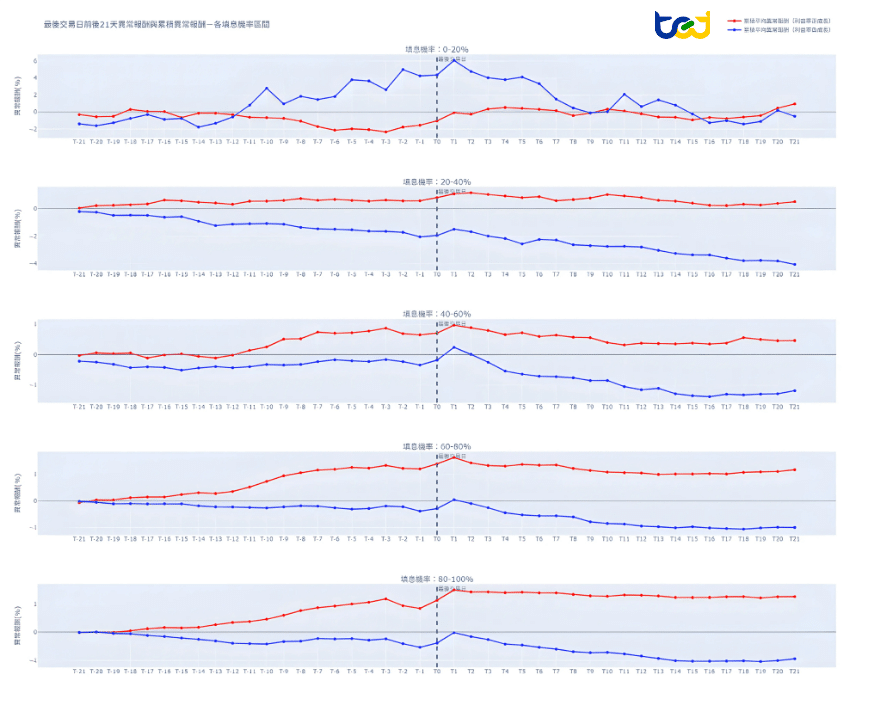
資料來源：TEJ資料庫整理

圖五、各填息機率區間正負營業利益成長率樣本公司最後交易日前後AAR(%)

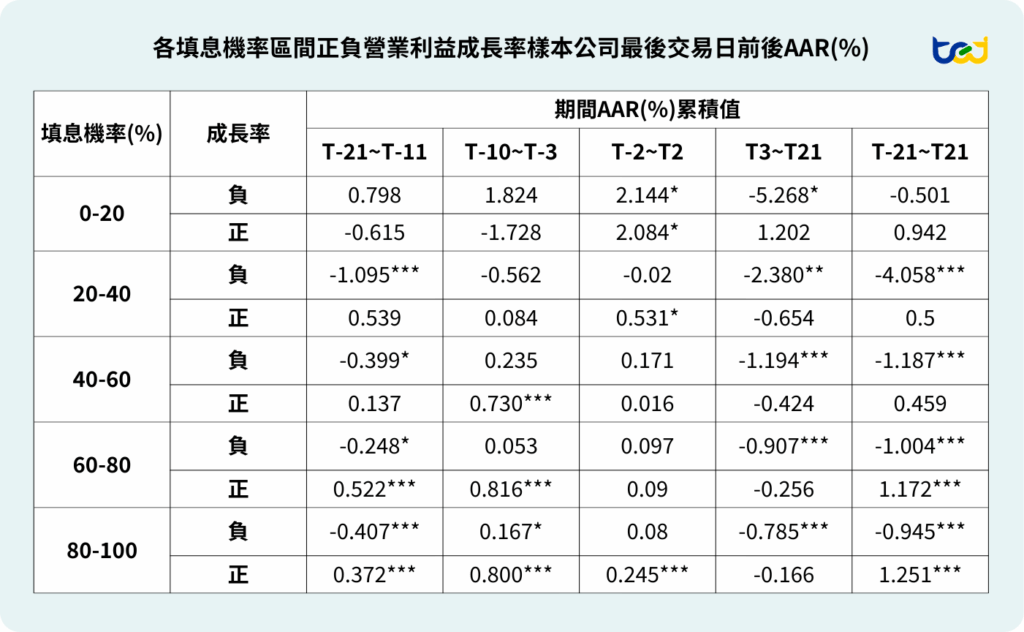
註：成長率為正代表公司於最後買進日時，最新一季的營業利益成長率大於零，反之則為負。

資料來源：TEJ資料庫整理

結論

整體來說，填息機率較高（40~100%）的股票在最後買進日（T）前一至兩週（T-10~T-3）間會出現顯著的買進潮，帶動股票報酬顯著高過同期大盤報酬，若進一步搭配財務指標如營業利益成長率進行區分則更為顯著。而在除息日後三天至一個月期間（T3~T21），就算是填息率高的股票，若非本業上有所增長，股價在後續走勢將顯著低於大盤。

因此，本研究歸納投資人若要挑選除息後能穩定填息又能長期持有之標的，除了參考過往的填息機率外，亦可選擇公司本業上有所進步之標的，從而減少股票在後續走低的可能性。此外，投資人亦可考慮在最後買進日前一個月或是除息公告日時就進場布局，並在最後買進日前一至兩天股價處於相對高點時進行賣出，利用多數散戶追逐高股利的心態賺取資本利得。

※溫馨提醒，本次研究與標的僅供參考，不代表任何商品或投資上的建議。

透過TEJ API輕鬆存取台灣財金資料庫

TEJ API，提供全方位財經資訊程式資料介接 API，資料涵蓋各類經濟、金融、股市、債市、期貨等多元化資料和分析工具。TEJ API以其豐富的數據庫和專業的分析功能，廣泛應用於金融機構、研究單位和投資者。

您可透過API靈活運用資料，或也可直接利用TQuant Lab回測系統．讓您的策略研究更有效率。

TQuant Lab 回測系統

TQuant Lab 提供專業的回測工具以及因子分析模組，透過TEJ專為量化投資者打造的TEJ API，整合回測工具，讓投資人可以用簡單的程式架構去實現心中的交易策略。

延伸閱讀

事件型因子研究：公司宣告發放股利